A −4.0μC charge is located 0.30 m to the left of a + +6.0μC charge. What is the magnitude and direction of the electrostatic force on the positive charge ?
2.4N to the right
2.4N to the left
4.8N to the right
4.8N to the left
The correct Answer is:B
To solve the problem, we will use Coulomb's Law, which states that the electrostatic force F between two point charges is given by the formula:
F=k|q1⋅q2|r2
where:
- F is the magnitude of the force between the charges,
- k is Coulomb's constant, approximately 9×109N m2/C2,
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
Step 1: Identify the charges and distance
We have:
- Charge q1=+6.0μC=+6.0×10−6C
- Charge q2=−4.0μC=−4.0×10−6C
- Distance r=0.30m
Step 2: Substitute values into Coulomb's Law
Using the values in Coulomb's Law:
F=k|q1⋅q2|r2
Substituting the values:
F=9×109|(6.0×10−6)⋅(−4.0×10−6)|(0.30)2
Step 3: Calculate the product of the charges
Calculate |q1⋅q2|:
|q1⋅q2|=|(6.0×10−6)⋅(−4.0×10−6)|=24.0×10−12C2
Step 4: Calculate r2
Calculate r2:
r2=(0.30)2=0.09m2
Step 5: Substitute into the equation
Now substitute back into the equation for F:
F=9×10924.0×10−120.09
Step 6: Calculate the force
Now perform the calculation:
F=9×109⋅24.0×10−120.09=9×109⋅2.6667×10−10=2.4N
Step 7: Determine the direction of the force
Since the positive charge (+6.0 µC) is attracted to the negative charge (-4.0 µC), the direction of the force on the positive charge will be towards the left (towards the negative charge).
Final Answer
The magnitude of the electrostatic force on the positive charge is 2.4N and the direction is towards the left.
---
- F is the magnitude of the force between the charges,
- k is Coulomb's constant, approximately 9×109N m2/C2,
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
We have:
- Charge q1=+6.0μC=+6.0×10−6C
- Charge q2=−4.0μC=−4.0×10−6C
- Distance r=0.30m
Using the values in Coulomb's Law:
Calculate |q1⋅q2|:
Calculate r2:
Now substitute back into the equation for F:
Now perform the calculation:
Since the positive charge (+6.0 µC) is attracted to the negative charge (-4.0 µC), the direction of the force on the positive charge will be towards the left (towards the negative charge).
The magnitude of the electrostatic force on the positive charge is 2.4N and the direction is towards the left.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Linked Comprehension)
5 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Problems
63 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
A particle of charge 3.00μC is separated by 0.120 m from a particle of charge −1.50μC. (a) What is the magnitude of the electrostatic force between them ? (b) What must their separation be to reduce that force by an order of magnitude ?
View SolutionEqual charges of +4μC are placed at the three corners of an equilateral triangle of side 2m. Calculate the magnitude and direction of the force on one of the charges.
View Solution
Knowledge Check
A charge of −3.00μC is fixed at the center of a compass. Two additional charges are fixed on the circle of the compass (radius 0.100 m). The charges on the circle are −4.00μC at the position due north and +5.00μC at the position due east. what is the magnitude and direction of the net electrostatic force acting on the charge at the center ? Specify the direction relative to due east.
A3.60N,51.3∘ north of eastB34.6N,36.3∘ north of eastC14.4N,44.2∘ north of eastD17.3N,38.7∘ south of eastA charge +q is located at the origin, while an identical charge is located on the x axis at x = +0.50 m. A third charge of +2 q is located on the x axis at such a place that the net electrostatic force on the charge at the origin doubles, its direction remaining unchanged. Where should the third charge be located ?
A+0.50mB+0.71mC−0.50mD−0.71m
A negative charge of magnitude 2 μC is moving with a speed of 3×106m/s along the positive Y-axis . A magnetic field →B=(0.5ˆi−0.4ˆk) T acts in the space.
What is the magnitude and direction of force on the given charge ?
View SolutionThere are two point charges +4 mu C and -2 mu C .The ratio of magnitude of electrostatic forces acting on them respectively will be
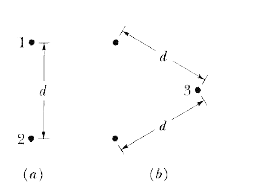
View SolutionIn Fig., particles 1 and 2 have charge 20.0μC each and are held at separation distance d = 0.75 m. (a) What is the magnitude of the electrostatic force on particle 1 due to particle 2? In Fig., particle 3 of charge 20.0μC is positioned so as to complete an equilateral triangle. (b) What is the magnitude of the net electrostatic force on particle 1 due to particles 2 and 3 ?
View SolutionThe charges and coordinates of two charged particles held fixed in an xy plane are q1=+3.0μC,x1=3.5cm,y1=0.50cm, and q2=−4.0μC,x2=−2.0cm,y2=1.5cm. Find the (a) magnitude and (b) direction of the electrostatic force on particle 1 due to particle 2. At what (c ) x and (d) y coordinates should a third particle of charge q3=+6.0μC be placed such that the net electrostatic force on particle 1 due to particles 2 and 3 is zero ?
View SolutionTwo point charges +4 μC and -4 μC are place(at vertices P and Q respectively of a right angled triangle. Calculate the magnitude and direction of electric field at a point R, if ∠PQR=90∘, PQ =0.03 cm and QR = 0.04 cm.
View SolutionThree Charges of magnitude 100μC are placed at the corners A, Band C ofan equilateral triangle of side 4m. If the charge at A and Care positive and the one at point B is negative, what is the magnitude and direction of total force acting on charge at C? [5.625N]
View Solution
