The students of class X of a school undertook to work for the campaign 'Say No to plastic' in a city. They took the map of the city and form coordinate plane on it to divide their areas. Group A took the region covered between the coordinates (1,1),(-3,2),(-2,-2) and (1,-3) taken in order. Find the area of the region covered by group A.
(i) What are the harmful effects of using plastic ?
(ii) How can you contribute in spreading awareness for such campaign ?
The correct Answer is:13.5 Square units
(i) Plastic is non-biodegradable and causes pollution.
(ii) By preparing posters or plays to spread awareness in the society.
To find the area of the region covered by Group A, we will use the coordinates provided: (1, 1), (-3, 2), (-2, -2), and (1, -3). We can divide the area into two triangles and calculate the area of each triangle separately.
Step 1: Identify the coordinates
The coordinates of the vertices of the polygon are:
- A(1, 1)
- B(-3, 2)
- C(-2, -2)
- D(1, -3)
Step 2: Divide the polygon into triangles
We can divide the quadrilateral into two triangles:
1. Triangle 1: A(1, 1), B(-3, 2), C(-2, -2)
2. Triangle 2: A(1, 1), C(-2, -2), D(1, -3)
Step 3: Calculate the area of Triangle 1 (A, B, C)
Using the formula for the area of a triangle given by vertices (x1, y1), (x2, y2), (x3, y3):
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Substituting the coordinates of Triangle 1:
- x1=1,y1=1
- x2=−3,y2=2
- x3=−2,y3=−2
Area1=12|1(2−(−2))+(−3)(−2−1)+(−2)(1−2)|
=12|1(4)+(−3)(−3)+(−2)(−1)|
=12|4+9+2|=12|15|=152=7.5 square units
Step 4: Calculate the area of Triangle 2 (A, C, D)
Using the same formula for Triangle 2:
- x1=1,y1=1
- x2=−2,y2=−2
- x3=1,y3=−3
Area2=12|1(−2−(−3))+(−2)(−3−1)+1(1−(−2))|
=12|1(1)+(−2)(−4)+1(3)|
=12|1+8+3|=12|12|=122=6 square units
Step 5: Calculate the total area
Now, we add the areas of both triangles:
Total Area=Area1+Area2=7.5+6=13.5 square units
Final Answer
The area of the region covered by Group A is 13.5 square units.
---
The coordinates of the vertices of the polygon are:
- A(1, 1)
- B(-3, 2)
- C(-2, -2)
- D(1, -3)
We can divide the quadrilateral into two triangles:
1. Triangle 1: A(1, 1), B(-3, 2), C(-2, -2)
2. Triangle 2: A(1, 1), C(-2, -2), D(1, -3)
Using the formula for the area of a triangle given by vertices (x1, y1), (x2, y2), (x3, y3):
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Substituting the coordinates of Triangle 1:
- x1=1,y1=1
- x2=−3,y2=2
- x3=−2,y3=−2
=12|1(4)+(−3)(−3)+(−2)(−1)|
=12|4+9+2|=12|15|=152=7.5 square units
Using the same formula for Triangle 2:
- x1=1,y1=1
- x2=−2,y2=−2
- x3=1,y3=−3
=12|1(1)+(−2)(−4)+1(3)|
=12|1+8+3|=12|12|=122=6 square units
Now, we add the areas of both triangles:
Total Area=Area1+Area2=7.5+6=13.5 square units
The area of the region covered by Group A is 13.5 square units.
Topper's Solved these Questions
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-IV : (Geometry)3videos
VALUE-BASED QUESTIONS
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-V : (Trigonometry)4videos
VALUE-BASED QUESTIONS
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-II : (Algebra)15videos
VALUE-BASED QUESTIONS
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SELF ASSESSMENT TEST10videos
TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
The area of the region bounded by y = x - 1 and x=3−y2 is
A52B72C92D4 - Question 2 - Select One
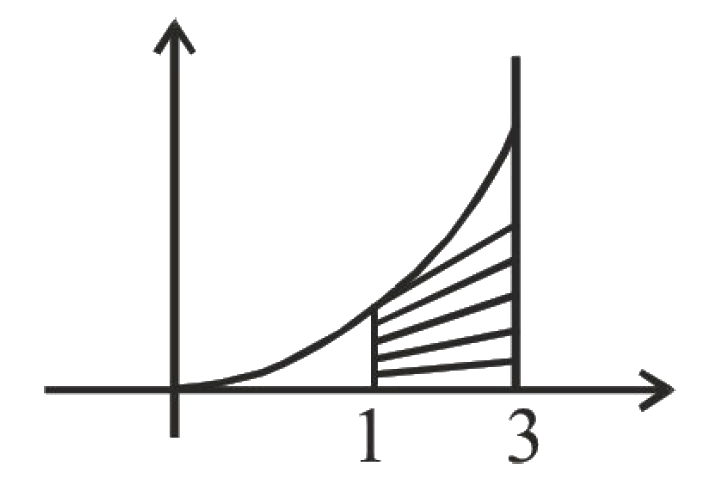
Find the area under the shaded region for curve y=3x2.A80B26C20D40 - Question 3 - Select One
The area of the region bounded by y=x−5 with the coordinate axis is
A25 sq unitsB12.5 sq unitsC50 sq unitsD20 sq units
Find the area of the region given by x24+y29≤1 and 3|x|+2|y|≥6.
View SolutionDraw a rough sketch to indicate the region bounded between the curve y2=4ax and the line x=3. also, find the area of this region.
View SolutionUsing integration, find the area of the region enclosed between the circles x2+y2=1 and (x−1)2+y2=1
View SolutionSketch the curves and identify the region bounded by the curves x=12,x=2,y=logxany=2x. Find the area of this region.
View SolutionArea of the region enclosed between the curves x=y2−1 and x=|y|√1−y2 is
View Solution
