Find maximum value of 1secθ,0∘≤θ≤90∘ .
The correct Answer is:1
To find the maximum value of 1secθ for 0∘≤θ≤90∘, we can follow these steps:
Step 1: Rewrite the expression
We know that the secant function is the reciprocal of the cosine function. Therefore, we can rewrite the expression as:
1secθ=cosθ
Step 2: Analyze the cosine function
The cosine function, cosθ, varies between 1 and 0 as θ changes from 0∘ to 90∘:
- At θ=0∘, cos0∘=1
- At θ=90∘, cos90∘=0
Step 3: Determine the maximum value
Since cosθ decreases from 1 to 0 in the interval (0∘,90∘), the maximum value of cosθ occurs at θ=0∘:
Maximum value of cosθ=cos0∘=1
Step 4: Conclusion
Thus, the maximum value of 1secθ in the given range is:
1
We know that the secant function is the reciprocal of the cosine function. Therefore, we can rewrite the expression as:
1secθ=cosθ
The cosine function, cosθ, varies between 1 and 0 as θ changes from 0∘ to 90∘:
- At θ=0∘, cos0∘=1
- At θ=90∘, cos90∘=0
Since cosθ decreases from 1 to 0 in the interval (0∘,90∘), the maximum value of cosθ occurs at θ=0∘:
Maximum value of cosθ=cos0∘=1
Thus, the maximum value of 1secθ in the given range is:
1
Topper's Solved these Questions
- INTRODUCTION TO TRIGONOMETRYBOOK - VK GLOBAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - SHORT ANSWER QUESTIONS-II
31 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - VK GLOBAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - LONG ANSWER QUESTIONS
13 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - VK GLOBAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - SELF - ASSESSMENT TEST
9 Videos
- HEIGHT AND DISTANCEBOOK - VK GLOBAL PUBLICATIONCHAPTER - HEIGHT AND DISTANCEEXERCISE - SELF ASSESSMENT TEST
11 Videos
- MID TERM TEST PAPER BOOK - VK GLOBAL PUBLICATIONCHAPTER - MID TERM TEST PAPER EXERCISE - SECTION -D
7 Videos
Similar Questions
Knowledge Check
If sinθ+cosecθ=2,then the value of sin5θcosec5θ,when 0∘≤θ≤90∘, is
A0B1C10D2If cosθ=513, then find the value of tan2θ+sec2θ.
0∘<θ<90∘&tanθ=√6+√6+√6+....∞, then find the value of sec2θ.A(a) 3923B(b) 3925C(c) 31325D(d) 32921The value of θ , which satisfies the equation tan2θ+3=3secθ,0∘≤θ<90∘ is
A45∘ व 0∘B60∘ व 0∘C15∘ व 0∘D30∘ व 0∘
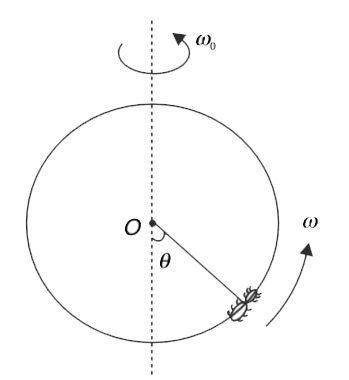
A ring is made to rotate about its diameter at a constant angular speed of ω0 . A small insect of mass m walks along the ring with a uniform angular speed ω relative to the ring (see figure). Radius of the ring is R.
(a) Find the external torque needed to keep the ring rotating at constant speed as the insect walks. Express your answer as a function of θ. For what value of q is this torque maximum? [given your answer for 0≤θ≤90∘ ]
(b) Find the component of force perpendicular to the plane of the ring, that is applied by the ring on the insect. For what value of θ is this force maximum? Argue quantitatively to show that indeed the force should be maximum for this value of θ. [Give your answer for 0∘≤θ≤90∘ ]
View SolutionIf sin2θ=cosθ, where0∘≤θ≤90∘, then θ=
View SolutionIf secθ=x+14x(0∘<θ<90∘) equal to
View SolutionFor 0≤θ≤π2 the maximum value of sinθ+cosθ is
View SolutionIf 7sin2θ+3cos2θ=4, then the value of cosθ(0∘≤θ≤90∘) is
View Solution
