A motor cycle starts from rest and accelerates along a straight path at 2m/s2. At the starting point of the motor cycle there is a stationary electric siren. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was at rest ? (Speed of sound = 330ms−2)
147 m
196 m
49 m
98 m
The correct Answer is:D
Motor cycle, u = 0, a=2m/s2
Observer is in motion and source is at rest.
f' is the appeared frequency
f'=(υ−υ0υ−(−υS))f=(330−υ0330)f
⇒ f'f=(330−υ0330)
0.94ff=330−υ0330
υ0=19.8m/s≈20m/s
The distance of motor cycle is
S=υ20−u22a=(19.8)2−04=98 m
Topper's Solved these Questions
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:ASSERTION REASON TYPE QUESTIONS
Explore 11 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:MATCHING TYPE QUESTIONS
Explore 3 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:REVISION EXERCISES
Explore 107 Videos
- UNITS AND MEASUREMENTBook:MODERN PUBLICATIONChapter:UNITS AND MEASUREMENTExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
A particle starts from rest and moves with a constant acceleration along a straight path to attain 64 m s−1 in t s. If at t = (t + 3)s the speed is 76 ms−1, then find the acceleration of the particle and 't'.
View SolutionA motor cycle moving with a speed of 5m/s is subjected to an acceleration of 0.2m/s2. Calculate the speed of the motor cycle after 10 second, and the distance travelled in this time.
View Solution
Knowledge Check
A motorcycle starts from rest and accelerates along a straight line at 2.2ms2. The speed of sound is 330ms. A siren at the starting point remains stationary. When the driver hears the frequency of the siren at 90% of when motorcycle is stationary, the distance travelled by the motorcyclist is
A123.75 mB247.5 mC495 mD990 mA motor bike is initially at rest. It then starts and further accelerates by 3 m/s3. At the rest position or at the starting point of motion there is a loud strong and stationary electric siren. What will be the distance travelled by the bike if the biker hears the siren frequency at 80% of its value when the bike was at rest. Speed of sound = 340 m/s.
A770.7 mB467.8 mC234 mD500 mA body starts from rest and moves along a straight line path with uniform acceleration. The ratio of velocities at t = 1s and t = 2 s is ______.
A2:1B1:2C1:√2D√2:1
A motorboat starting from rest on a lake acceleration line at a constant rate of 3.0m/s2 for 8.0s. How far does the boat travel during this time ?
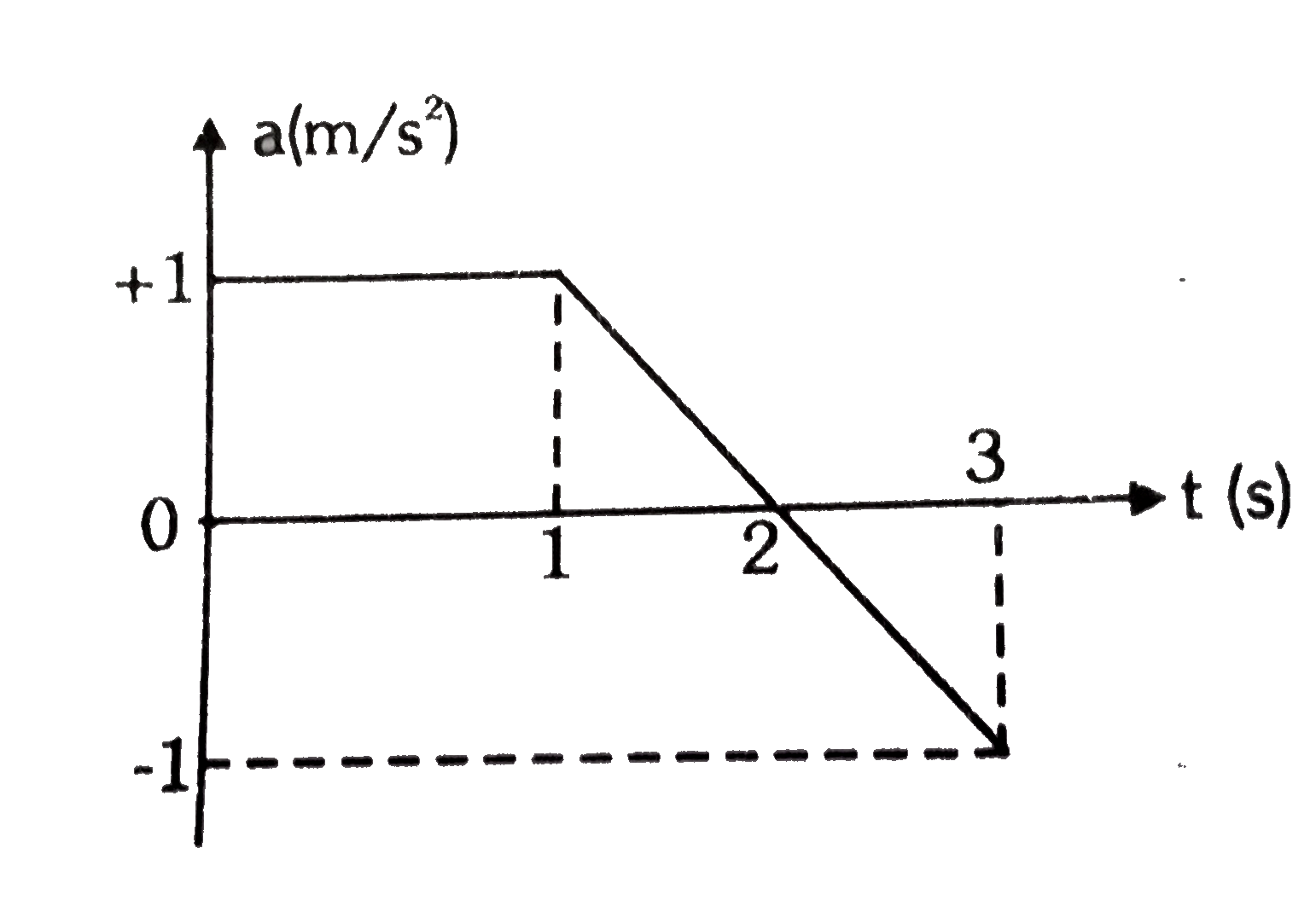
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
View SolutionA disc of radius 0.1 m starts from rest with an angular acceleration of 4.4rad/s2 .Then linear velocity of the point on its after 5 s is
View SolutionStarting from rest, a particle confined to move along a straight line is accelerated at a rate of 5.0 m/s2. Which one of the following statements accurately describes the motion of this particle ?
View Solution

