In Fig. 5-27, a block attached to a chord is resting on an inclined plane. Let the mass of the block be 8.5 kg and the angle θ be 30∘.
(a) Find the tension in the cord and normal force acting on the block.
(b) If the cord is cut, find the magnitude of the resulting acceleration of the block.
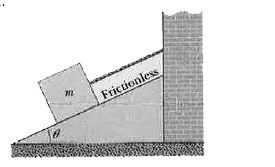
Figure 5-27 A block attached to a chord resting on an incline.
(1) We apply Newton.s second law to solve for the tension in the cord and the normal force on the block.
(2) The free-body diagram of the problem is shown in the Fig. 5-28. Since the acceleration of the block is zero, the components of Newton.s second law equation yield
T−mg sinθ=0 (5−39)
FN=mg cosθ=0, (5−40)
where T is the tension in the cord, and FN is the normal force on the block.
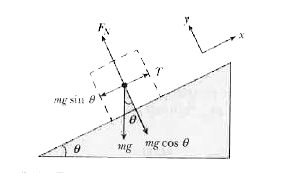
Figure 5.28 Free body diagram of the given problem.
Calculation: Solving Eq. (5-39) for the tension in the string, we find
T=mg sinθ=(8.5 kg)(9.8 m/s2)sin30∘
=42 N.
We solve Eq. (5-40) above for the normal force FN.
FN=mg cosθ=(8.5 kg)(9.8 m/s2)cos30∘
=72 N.
(b) If the cord is cut, find the magnitude of the resulting acceleration of the block.
Calculation: When the cord is cut, it no longer exerts a force on the block and the block accelerates. The x component of the second law becomes -mg sinθ=ma, so the acceleration becomes
a=−gsinθ=−(9.8 m/s2)sin30∘
=−4.9 m/s2.
The negative sign indicates the acceleration is down the plane. The magnitude of the acceleration is 4.9 m/s2.
Note: The normal force FN on the block must be equal to mg cosθ so that the block is in contact with the surface of the incline at all time. When the cord is cut, the block has an acceleration a=−gsinθ, which in the limit θ→90∘ becomes −g, as in the case of a free fall.
Topper's Solved these Questions
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT
5 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PROBLEMS
52 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )
5 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
Similar Questions
A block of mass 5 kg is acted upon two perpendicular force 7 N and 24N. Find the magnitude and the direction of acceleration of the block.
View SolutionA block of mass 2 kg is kept at rest on a smooth inclied plane as shown in (a) with the help of a string Find the tension in the string and reaction on the block if the string is cut, find the acceleration of the block neglecting friction.
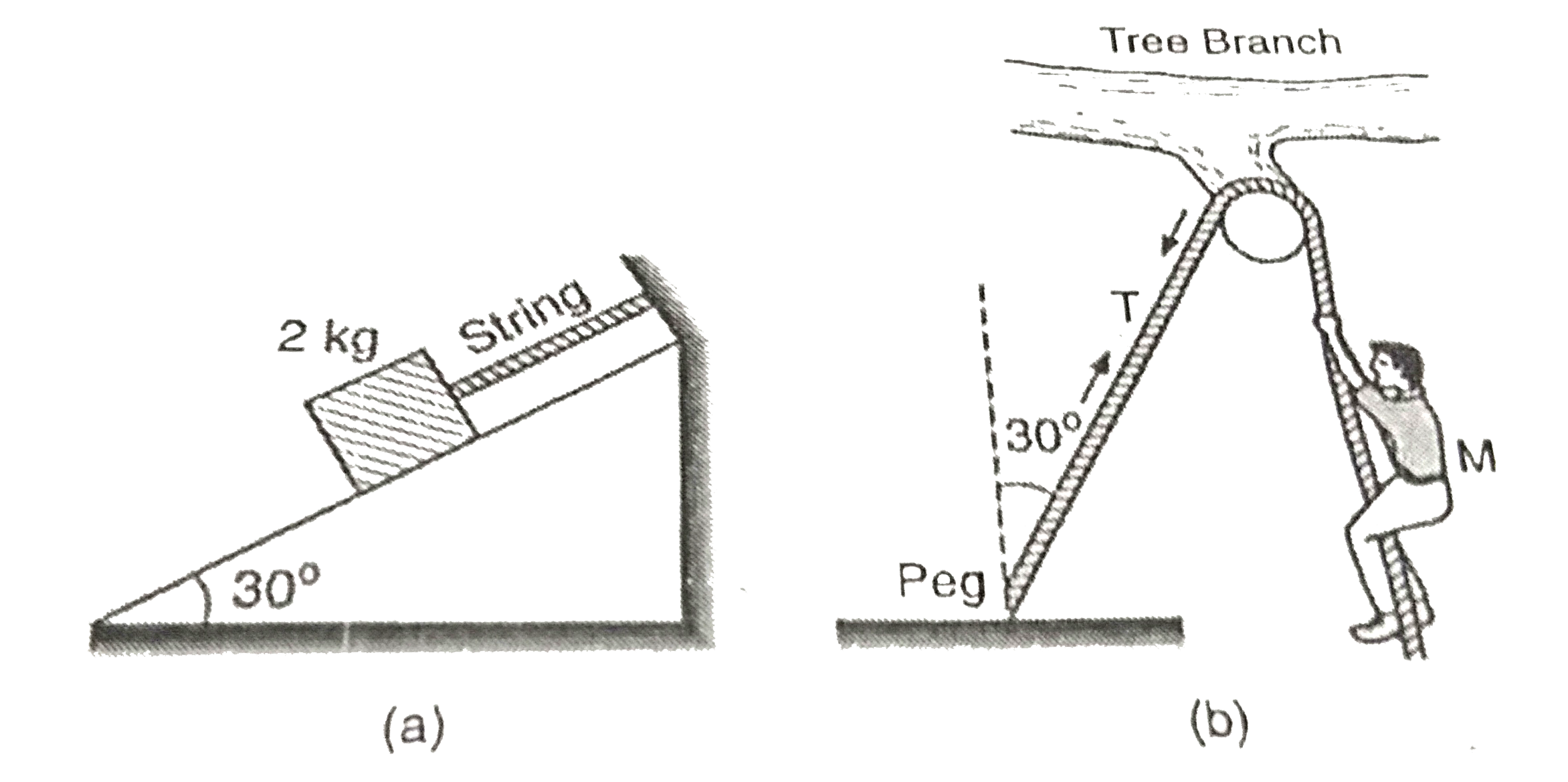
View Solution
Knowledge Check
Two forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?
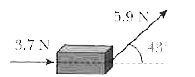 A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2
A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2The figure shows a horizontal force →F acting on a block of mass M on an inclined plane (angle θ). What is the normal reaction N on the block?
 Amgsinθ+FcosθBmgsinθ−FcosθCmgcosθ−FsinθDmgcosθ+Fsinθ
Amgsinθ+FcosθBmgsinθ−FcosθCmgcosθ−FsinθDmgcosθ+FsinθA block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
A2.5 NB0.98 NC4.9 ND0.49 N
In Fig. 6-52, two blocks, in contact, slide down an inclined plane AC of inclination 30∘ . The coefficient of kinetic friction between the 2.0 kg block and the incline is u1=0.20 and that between the 4.0 kg block and the incline is μ2=0.30. Find the magnitude of the acceleration.

View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block is placed on a rough horizontal plane. Three horizontalforces are applied on the block as shown in the figure. If the block is in equilibrium, find the friction force acting on the block.
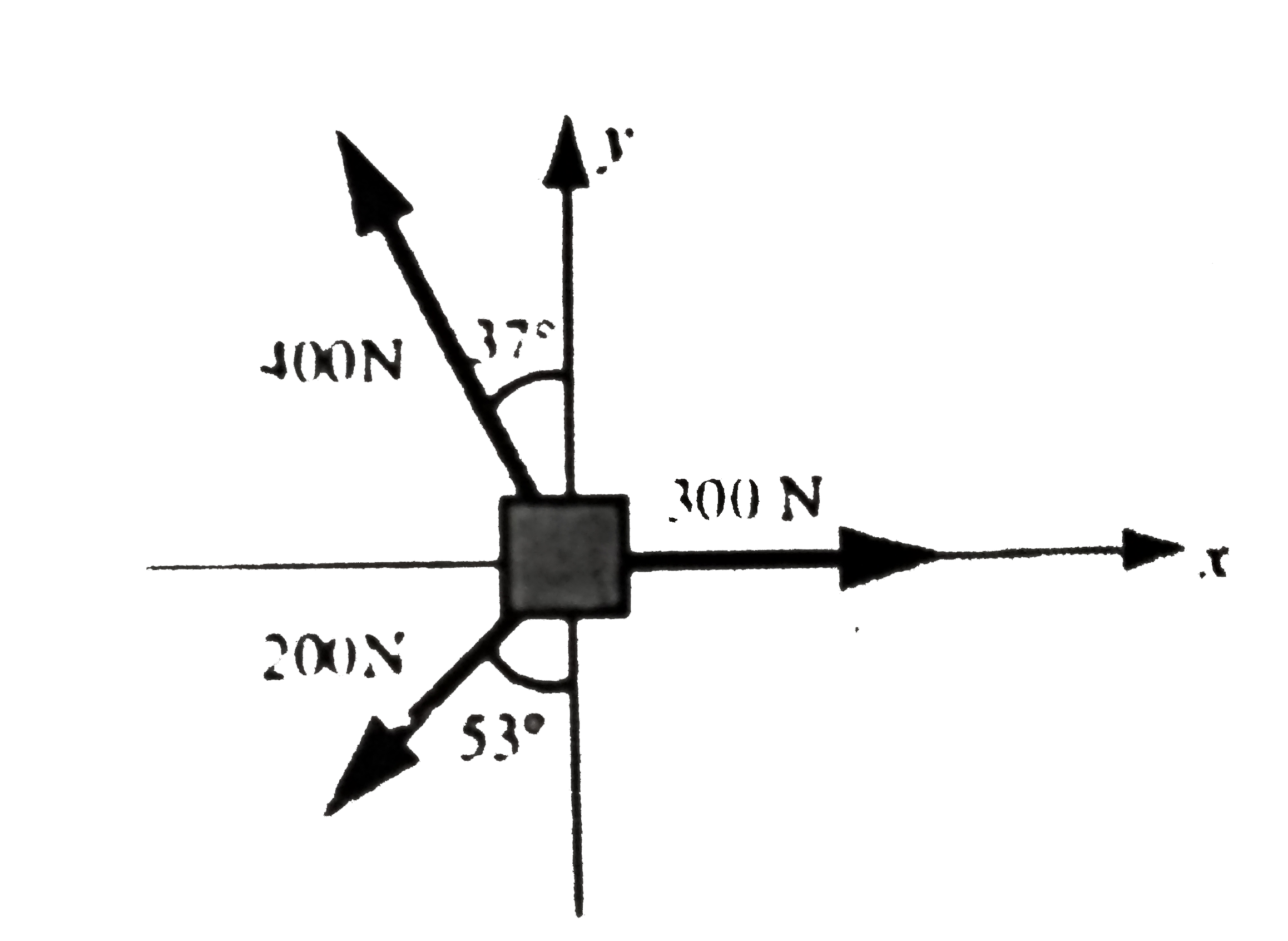
View SolutionA force of 50 N acts in the direction as shown in figure. The block of mass 5kg. Resting on a smooth horizonatal surface. Find out the acceleration of the block.
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
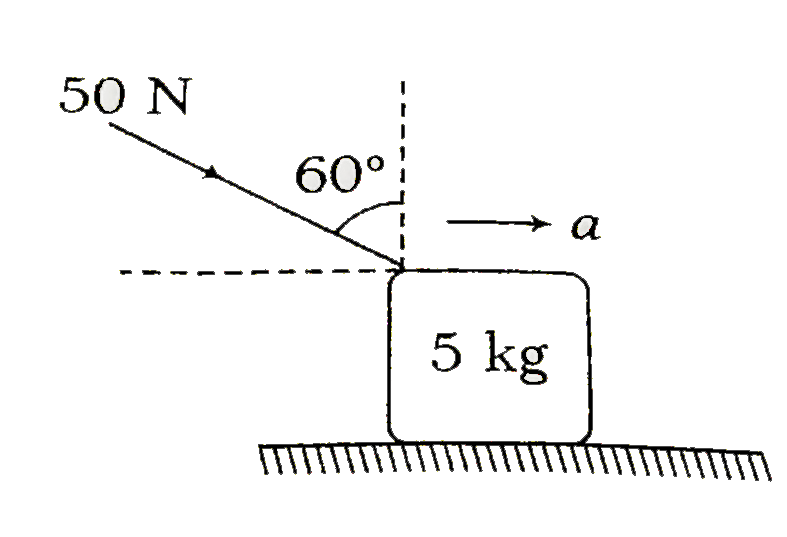
View Solution
