Find the values of $β$ so that the point $(0, β)$ lies on or inside the triangle havind the sides $3 x + y + 2 = 0, 2 x - 3 y + 5 = 0 a n d x + 4 y - 14 = 0 .$

A

$[\frac{5}{3}, \infty)$

B

$(- \infty, \frac{7}{2}]$

C

$[\frac{5}{3}, \frac{7}{2}]$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let ABC be the given triangle. The coordinates of the vertices of the triangle ABC are marked in fig. 12 . The point $P (0, β)$ will lie inside or on the triangle ABC, if the following three conditions hold simultaneously.
(i) A and P lie on the same side of BC,
(ii) B and P lie on the same side of AC,
(iii) C and P lie on the same side of AB.
Now, A and P will lie on the same side of BC, if
$(3 \times 2 + 3 + 2) (3 \times 0 + β + 2) > 0$
$\Rightarrow 11 (β + 2) \geq o \Rightarrow β + 2 \geq 0 \Rightarrow β \geq - 2 (i)$
B and P will lie on the same side of AC, if
$(- 2 \times 2 - 3 \times 4 + 5) (2 \times 0 - 3 β + 5) \geq 0$
$\Rightarrow - 11 (- 2 β + 5) \geq 0 \Rightarrow 3 β - 5 \leq 0 \Rightarrow β \geq \frac{5}{3} ... (i i)$

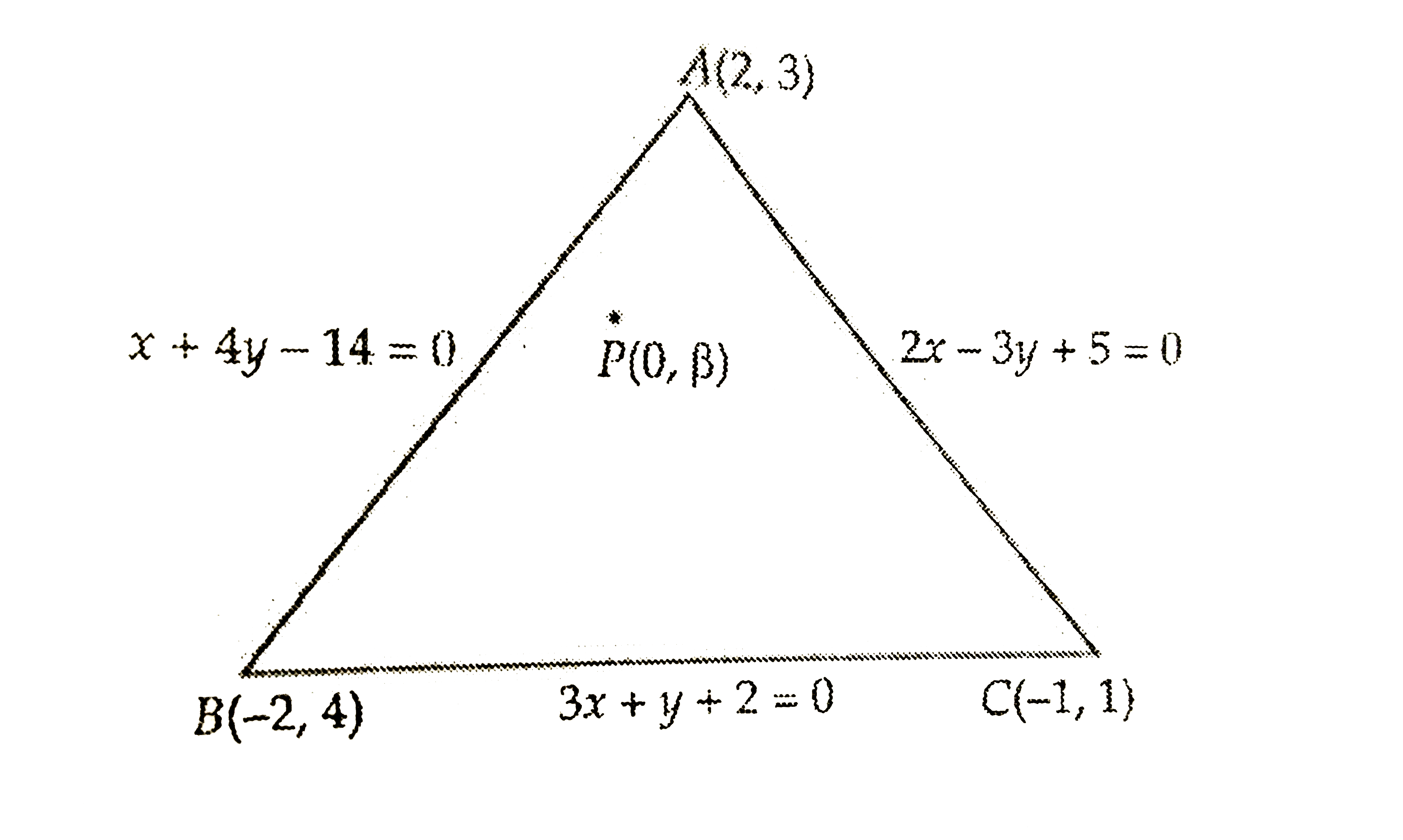
$(- 1 + 1 \times 4 - 14) (0 + 4 β - 14) \geq 0$
$\Rightarrow - 22 (2 β - 7) \geq 0 \Rightarrow 2 β - 7 \leq 0 \Rightarrow β \leq \frac{7}{2} ... (i i i)$
From (i), (ii) and (iii), we obtain that
$\frac{5}{3} \leq β \leq \frac{7}{2} i . e . β \in [\frac{5}{3}, \frac{7}{2}]$

Updated on:21/07/2023

|

Class 11 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Point $(0, β)$ lies on or inside the triangle fromed by the lines $y = 0, x + y = 8$ and $3 x - 4 y + 12 = 0$ . Then $β$ can be :
A2
B4
C8
D12

OBJECTIVE RD SHARMA-STRAIGHT LINES-Chapter Test

Home
Ask Doubt
Profile