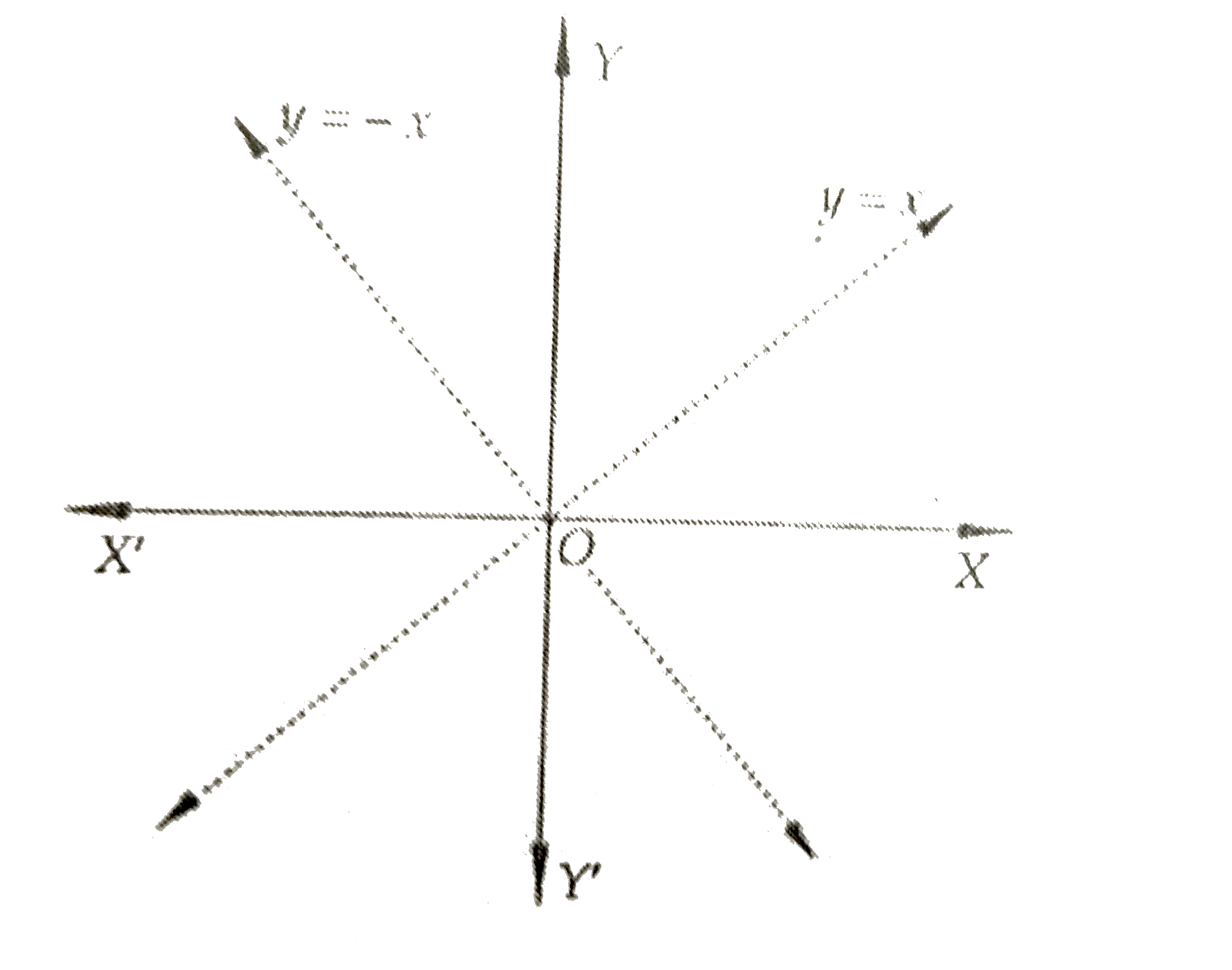
The equations of bisectors of the angles between the lines |x|=|y| are
y=±x,x=0
x=12,y=12
y=0,x=0
none of these
The correct Answer is:C
Given lines are |x|=|y| or y=±x. Clearly , these are the bisectors of the first and second quadrant angles. So, the bisectors of the angles between these lines are the coordinate axes i.e. x=0, y=0.
Topper's Solved these Questions
Similar Questions
Find the equations of bi sectors of the angle between the lines 4x + 3y = 7 and 24x + 7y-31- 0. Also find which of them is la) the bisector of the angle contaäining origin (b) the bisector of the acute angle.
View SolutionThe equation of the bisectors of the angles between the lines represented by the equation
2(x+2)2+3(x+2)(y−2)−2(y−2)2=0 is
View Solution
Knowledge Check
The equation of the bisector of that angle between the lines x + y = 3 and 2x - y = 2 which contains the point (1,1) is
A(√5−2√2)x+(√5+√2)y−3√5+2√2=0B(√5+2√2)x+(√5−√2)y−3√5−2√2=0C3x = 10Dnone of theseThe joint equation of bisectors of the angles between the lines given by 5x2+6xy−y2=0, is
Ax2+2xy+y2=0Bx2+2xy−y2=0Cx2−2xy+y2=0Dx2−2xy−y2=0The equation of the bisector of the acute angles between the lines 3x-4y+7 = 0 and 12 x + 5y -2 = 0 is :
A(a) 21x + 77y - 101 = 0B(b) 99x - 27y + 81 = 0C(c) 21x - 77y + 101 = 0D(d) None of the above
The combined equation of the bisectors of the angle between the lines represented by (x2+y2)√3=4xy is
View SolutionThe equation of the bisectors of the angle between the lines joining the origin to the points of intersection of the curve x2+xy+y2+x+3y+1=0 and the line x+y+2=0 is
View SolutionFind the equations of the bisectors of the angles, between the lines through (0,0) with slopes 1 and 2.
View SolutionThe equation of the bisector of the acute angles between the lines 3x-4y+7 = 0 and 12 x + 5y -2 = 0 is :
View SolutionThe equation(s) of the bisectors(s) of that angles between the lines x+2y−11=0,3x−6y−5=0 which contains the point (1,-3) is
View Solution
