Let A and B be two events such that p(¯¯¯A∪B)=16,p(A∩B)=14 and p(¯¯¯A)=14 , where ¯¯¯A stands for the complement of the event A. Then the events A and B are
independent but not equally likely
independent and equally likely
mutually exclusive and independent
equally likely but not independent
The correct Answer is:A
We have,
P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14 and P(¯¯¯A)=14
⇒1−P(A∪B)=16⇒(A∪B)=56
⇒P(A)+P(B)−P(A∩B)=56⇒34+P(B)−14=56
⇒P(B)=13
Now, P(A∩B)=14,P(A)=34 and P(B)=13
⇒P(A∩B)=P(A)P(B) and P(A)≠P(B)
⇒ A and B independen but not equally likely.
Topper's Solved these Questions
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section I - Solved Mcqs
126 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Section- II (Assertion -Reason Types MCQs)
15 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- QUADRATIC EXPRESSIONS AND EQUATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - QUADRATIC EXPRESSIONS AND EQUATIONS EXERCISE - Chapter Test
50 Videos
Similar Questions
Let A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14 where ¯¯¯A stands for complement of event A. Then, events A and B are
View SolutionLet A and B be two events such that
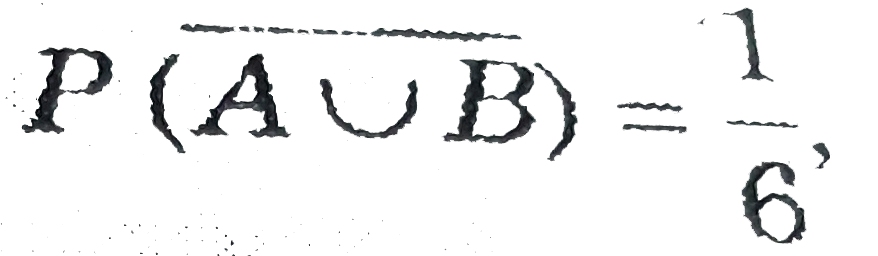 ,P(A cap B)=(1)/(4)andPoverset(-)(A)=(1)/(4),whereoverset(-)A stands for the complement of the event A. Then, the events A and B are
,P(A cap B)=(1)/(4)andPoverset(-)(A)=(1)/(4),whereoverset(-)A stands for the complement of the event A. Then, the events A and B are
View Solution
Knowledge Check
Let A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
Amutually exclusive and independentBequally likely but not independentCIndependent but not equally likelyDindependent and equally likelyLet A and B be two events such that P(¯¯¯¯¯¯¯¯¯¯A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where¯¯¯A stands for the complement of the event A. Then the events A and B are
Amutually exclusive and independentBequally likely but not independentCindependent but not equally likelyDindependent and equally likelyLet A and B be two events such that
P(A∩B)=16,P(A∪B)=3145 and P(¯¯¯B)=710, thenAA and B are independentBA and B are mutually exclusiveCP(AB)<16DP(BA)<16
Let A and B be the two events such that P(A)=12,P(B)=13andP(A∩B)=14 , find
P(AB)
View SolutionLet A and B be the two events such that P(A)=12,P(B)=13andP(A∩B)=14 , find
P(BA)
View SolutionLet A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP(¯¯¯A)=14,where ¯¯¯A stands for complement of event A. then , events A and B are
View SolutionIf A and B are any two events such that P(A∪B)=34,
P(A∩B)=14andP(¯¯¯A)=23, where ¯¯¯A stands for the complementary event of A, then what is P(B) ?
View SolutionIf A and B are two events such that P[(A∪B)']=16,P(A∩B)=14 and P(A')=14 , then events A and B are
View Solution
