A particle is moving uniformly in a circular path of radius r. When it moves through an angular displacement $θ$ , then the magnitude of the corresponding linear displacement will be

A

$2 r cos (\frac{θ}{2})$

B

$2 r cos (\frac{θ}{2})$

C

$2 r tan (\frac{θ}{2})$

D

$2 r sin (\frac{θ}{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

According to cosine formula

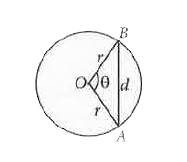
$cos θ = \frac{r^{2} + r^{2} - d^{2}}{2 r^{2}}$
$2^{2} cos θ = r^{2} + r^{2} - d^{2}$
$d^{2} = 2 r^{2} cos θ = 2 r^{2} [1 - cos θ]$
$[∴ cos θ = 1 - 2 \frac{{sin}^{2} θ}{2}]$
or $d = 2 r \frac{sin (θ)}{2}$
$∴$ Linear displacement, $A B = 2 r \frac{sin (θ)}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS LAWS OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is moving on a cicular path of radius 'R' . As it moves through an angular displacement $θ$ , its linear displacement will be :
A $R sin θ$
B $2 R cos θ / 2$
C $2 R sin θ / 2$
D $R cos θ$
Question 2 - Select One
A particle moves through angular displacement $θ$ on a circular path of radius' r'. The linear displacement will be:
A $2 r sin (\frac{θ}{2})$
B $2 r cos (\frac{θ}{2})$
C $2 r tan (\frac{θ}{2})$
D $2 r cot (\frac{θ}{2})$
Question 3 - Select One
A particle moves throught angular displacement $θ$ on a circlur path of radius r. The liner displacement wil be
A $2 r sin (θ / 2)$
B $2 r cos (θ / 2)$
C $2 r tan (θ / 2)$
D $2 r cot (θ / 2)$

MTG-WBJEE-LAWS OF MOTION -WB JEE PREVIOUS YEARS QUESTIONS (CATEROGY 1: SINGLE OPTION CORRECT TYPE (1 MARK))

Home
Ask Doubt
Profile