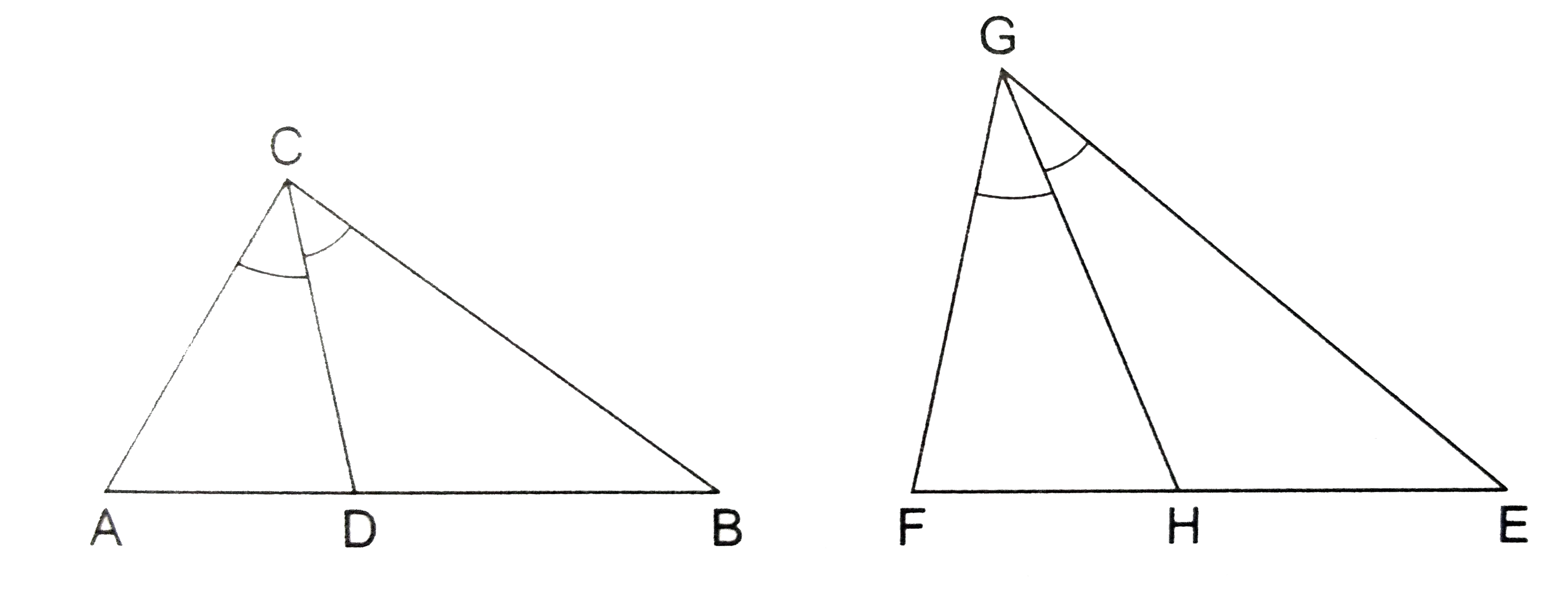
In the given figure, CD and GH are respectively the bisectors of ∠ACBand∠FGEofΔABCandΔEFG respectively . If ΔABC~ΔFEG, prove that :
(a) ΔADC~ΔFHG (b)ΔBCD~ΔEGH (c)CDGH=ACFG
Video Solution
Text Solution
ΔABC~ΔFEG (given)
∴∠ACB=∠FGE [ corresponding angles of similar triangles are equal]
⇒12∠ACD=12∠FGE.
(a) In ΔADCandΔFHG, we have
∠DAC=∠HFG[∴∠A=∠FsinceΔABC~ΔFEG]
and ∠ACD=∠FGH [ proved above]
∴ΔADC~ΔFHG [ by AA- similarity]
(b) In ΔBCDandΔEGH, we have
∠DBC=∠HEG[∴∠B=∠EsinceΔABC~ΔFEG]
and∠DCB=∠HGE [ proved above]
∴ΔBCD~ΔEGH.
(c) We have
ΔADC~ΔFHG [ proved above]
And so, CDGH=ACFG [ crossponding sides of similar triangles are proportional.]
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7A
12 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself
20 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
In a triangle, with usual notations, the length of the bisector of angle A is
A2bcb+csinA2B2bcb+ccosA2Cabc2R(b+c)cosecA2D4Ab+ccosecA2In given triangle ABC ,OB and OC are bisectors of ∠Ba nd ∠C respectively then ∠BOC is equal to
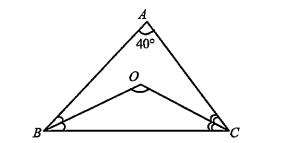 A70∘B110∘C140∘D80∘
A70∘B110∘C140∘D80∘
In the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
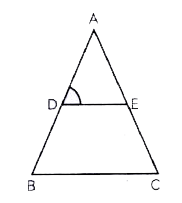
View SolutionIn the given figure, if ∠D=∠C, then it is true that △ADE~△ACB? Why?
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionIn ΔABC,DandE are the midpoint of AB and AC respectively. Find the ratio of the areas of ΔADEandΔABC.
View SolutionIn the given figure , AB=CD,CE=BF and ∠ACE=∠DBF . Prove that
△ACE≅△DBF
View SolutionIn a triangle aBC ,∠B=2∠C.AD and BE bisectors of ∠BACand∠ABC. If AB=CD . Find ∠BAC
View Solution