ABCD is a quadrilateral; P,Q,RandS are the points of trisection of side AB,BC,CDandDA respectively and are adjacent to AandC ; prove that PQRS is parallelogram.
GIVEN A quadilateral ABCD in which P,Q,R,S are the points of trisection of AB,BC, CD and DA respectively (as shown).
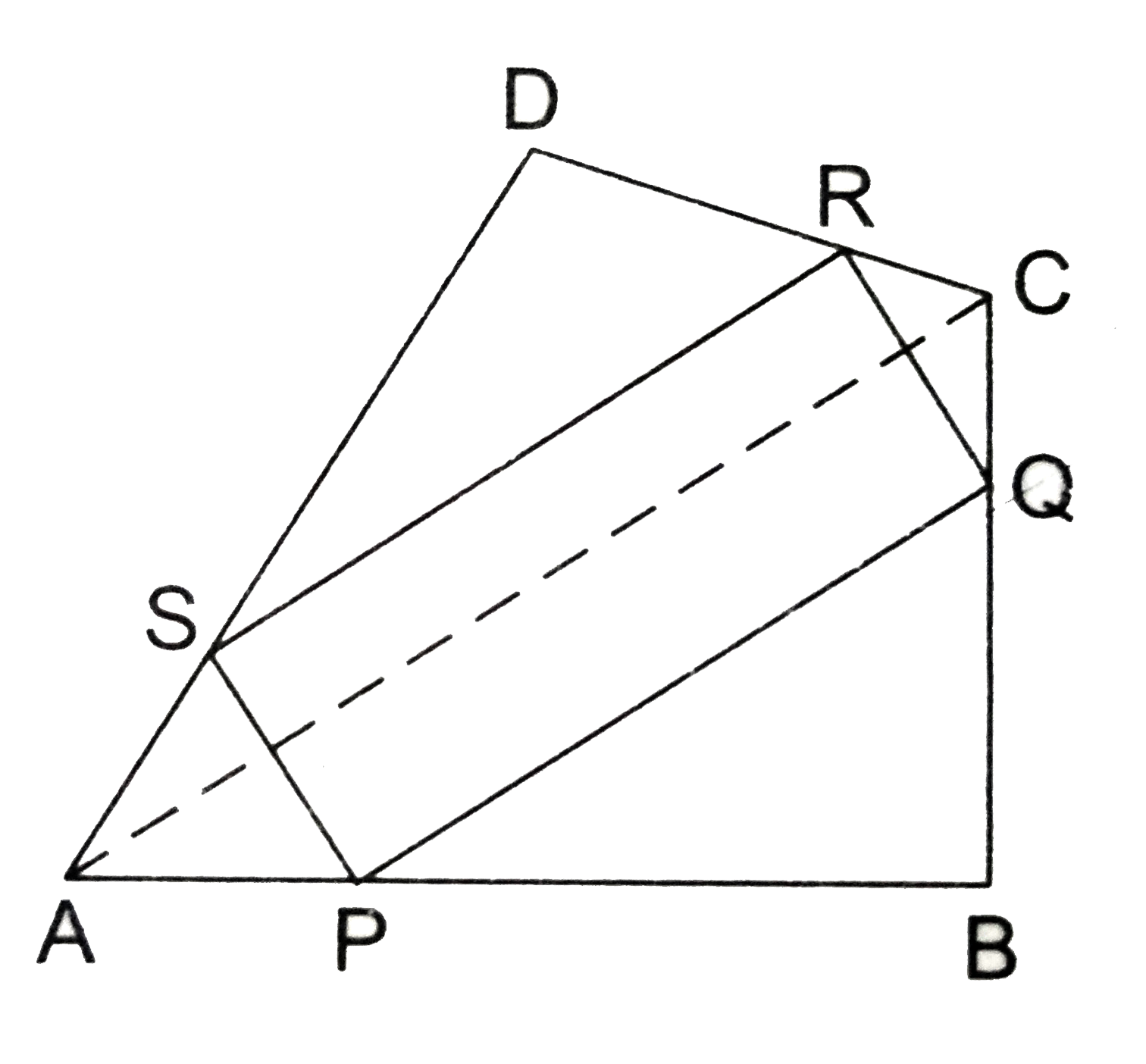
TO PROVE PQRS is paarallellorgam.
CONSRUCTION Join AC.
PROOF In ΔABC, we have BPPA=BQQC=21
∴PQ∣∣AC... (i) [ by the converse of Thale's theorm]
Also, in ΔDAC, we have
DSSA=DRRC=21
∴SR∣∣AC...... (ii) [ by the converse of Thale's theorm]
Thus, PA∣∣SR [ from (i) and (ii)]
Similarly, by joining BD we can prove that SP∣∣RQ.
Hence, PQRS is a parallelogram.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE4videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A1videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
ABCD is a quadrilateral; P,Q,RandS are the points of trisection of side AB,BC,CDandDA respectively and are adjacent to AandC ; prove that PQRS is parallelogram.
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
 View Solution
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionIf D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View Solution

