The angle of elevation of an aeroplane from a point P on the ground is $60^{\circ}$ . After a flight of 15 seconds, the angle of elevation changes to $30^{\circ}$ . If the aeroplane is flying at a constant height of $1500 \sqrt{3}$ m, find the speed of the aeroplane

Video Solution

Text Solution

Verified by Experts

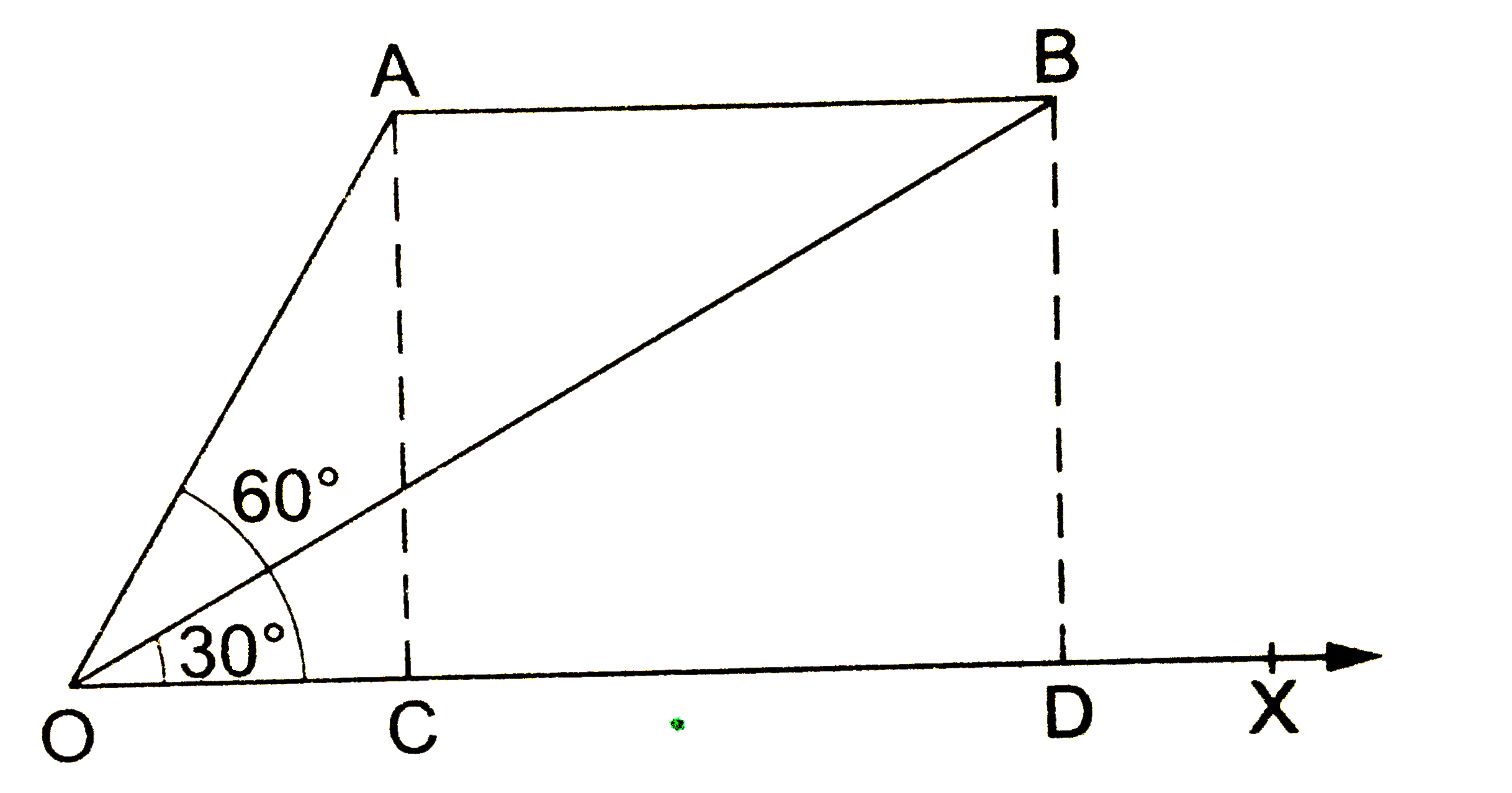
Let OX be the horizontal ground and let O be the point of observation. Let A and B be the two positions of the aeroplane.
Let $A C ⊥ O X$ and $B D ⊥ O X$ . Then,
$∠ C O A = 60^{\circ}, ∠ D O B = 30^{\circ}$ .
and $A C = B D = 1500 \sqrt{3} m$ .
From right $Δ O C A$ , we have
$\frac{O C}{A C} = {cot 60}^{\circ} = \frac{1}{\sqrt{3}}$ .
$\Rightarrow \frac{O C}{1500 \sqrt{3}} = \frac{1}{\sqrt{3}} \Rightarrow O C = 1500 m$ .
From right $Δ O D B$ , we have
$\frac{O D}{B D} = {cot 30}^{\circ} = \sqrt{3} \Rightarrow \frac{O D}{1500 \sqrt{3 m}} = \sqrt{3}$ .
$\Rightarrow O D = (1500 \times 3) m = 4500 m$ .
$∴ C D = (O D - O C) = (4500 - 1500) m = 3000 m$ .
Thus, the aeroplane covers $300 m$ in $15$ seconds.
$∴$ speed of the aeroplane $= (\frac{3000}{15} \times \frac{60 \times 60}{1000}) k m / h r$
$= 720 k m / h r$ .
Hence, the speed of the aeroplane is $720 k m / h r$ .

Updated on:21/07/2023

The angle of elevation of an airplane from a point on the ground is $60^{\circ}$ . After a flight of $30$ seconds, the angle of elevation becomes $30^{\circ}$ . If the airplane is flying at a constant height of $3000 \sqrt{3}$ m, find the speed of the airplane.
A $200 m / s$
B $250 m / s$
C $350 m / s$
D $300 m / s$
The angle of elevation of an aeroplane from a point on the ground is $60^{\circ}$ .After flying for 30 seconds ,the angle of elevation changes to $30^{\circ}$ .If the aeroplane is flying at a height of $1500 \sqrt{3}$ metre , then what is the speed (in m/s) of aeroplane?
A50
B100
C200
D300
The angle of elevation of an aeroplane from a point on the ground is $60^{\circ}$ . After flying for 30 seconds, the angle of elevation charges to $30^{\circ}$ . If the aeroplane is flying at a height of 4500 m, then what is the speed (in m/s) of aeroplane
A $50 \sqrt{} 3$
B $100 \sqrt{} 3$
C $200 \sqrt{} 3$
D $300 \sqrt{} 3$