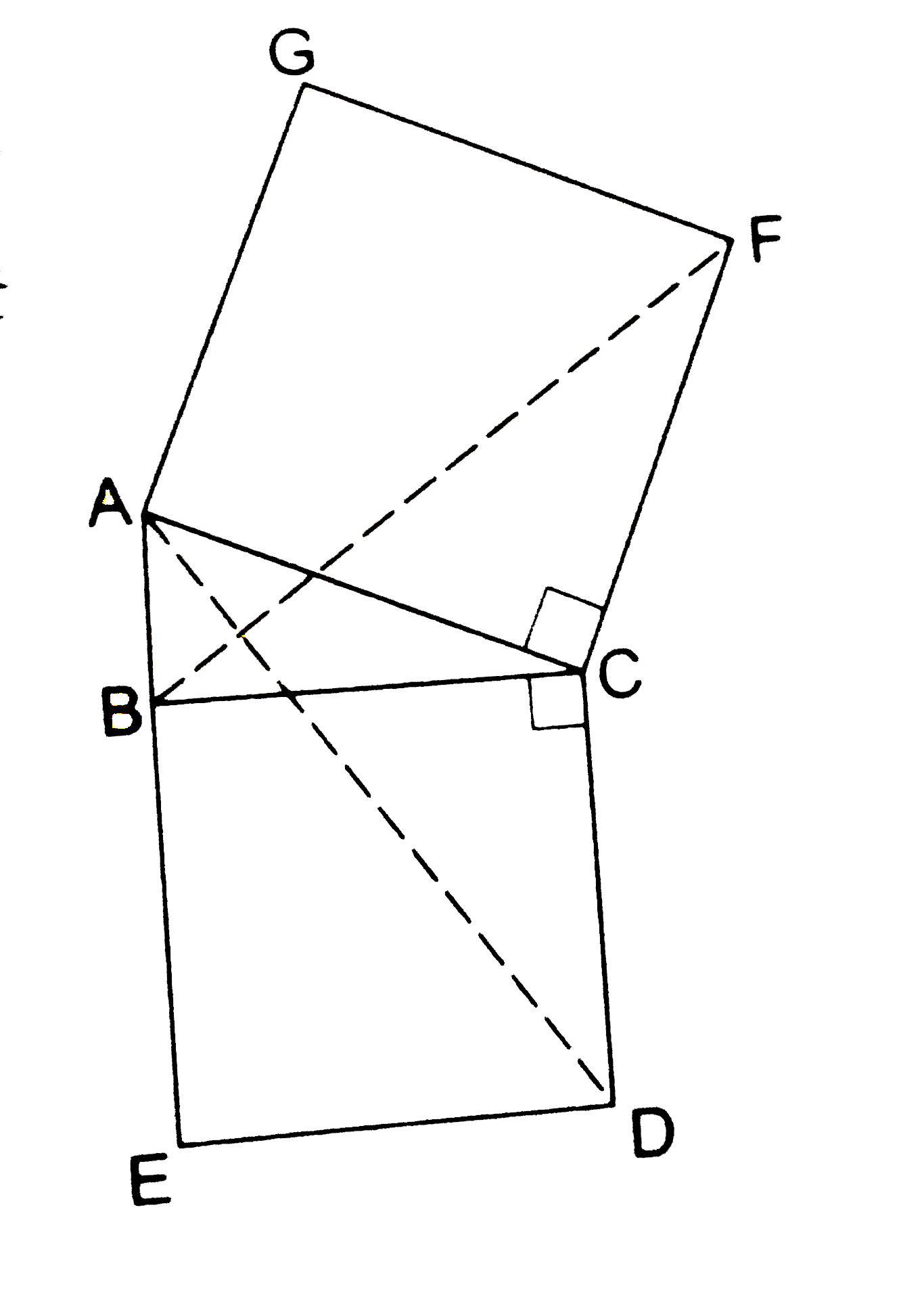
In the given figure, ABC is a triangle, right angled at B. If BCDE is a square on side BC and ACFG is a square on AC, prove that AD = FB.
Video Solution
Text Solution
In ΔACDandΔFCB, we have
∠ACD=90∘+∠BCA
and∠FCB=90∘+∠BCA
⇒ ∠ACD=∠FCB
CA=CF (sides of the same square)
CD=CB (sides of the same square)
∴ ΔACD≅ΔFCB (SAS-criteria).
Hence, AD=FB (c.p.c.t.).
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
In the adjoining figure ABC is a right angled triangle, BDEF is a square, AE = 7.5 cm and AC = 18 cm. What is the area of triangle ABC?
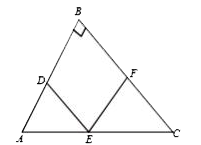 A76.621cm2B70.054cm2C83.25cm2D90.00cm2
A76.621cm2B70.054cm2C83.25cm2D90.00cm2
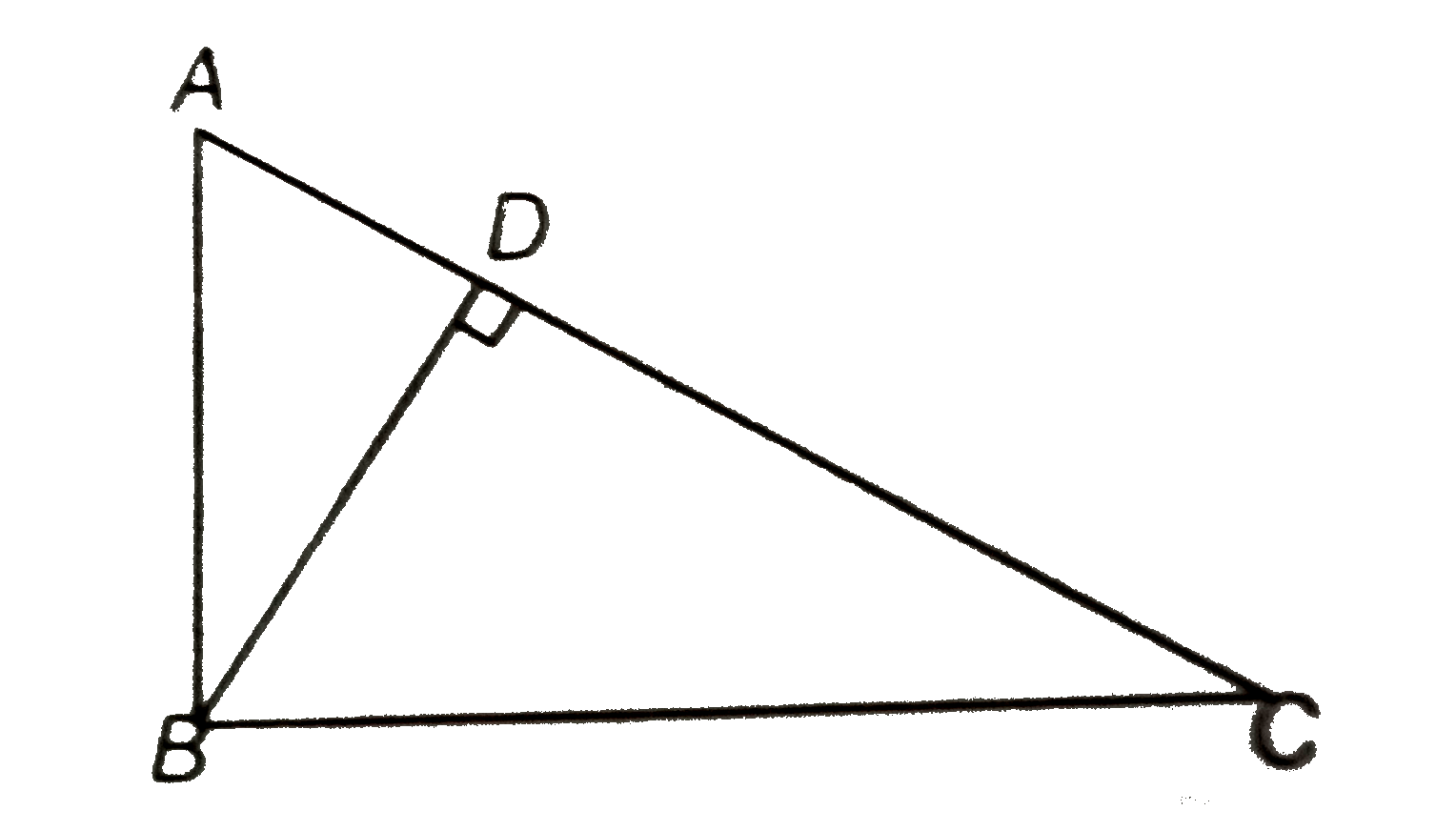
In the figure given below ABC is a triangle right angled at A and AC ⊥ CD . Show that
AC2=BC×DC
View SolutionIn the given figure,ABC in a right-angled triangle,right-angled atB.IfBC=5cmandAC-AB=1cm,f∈dthevalueofcosecAandcos A
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
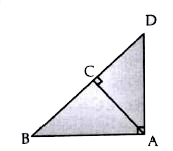
AB2=BC×BD
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
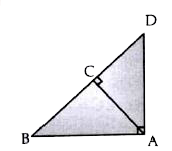
AD2=BD×DC
View SolutionIn the given figure, in ΔABC,∠B=∠CandBD=CE. Prove that DE∣∣BC.
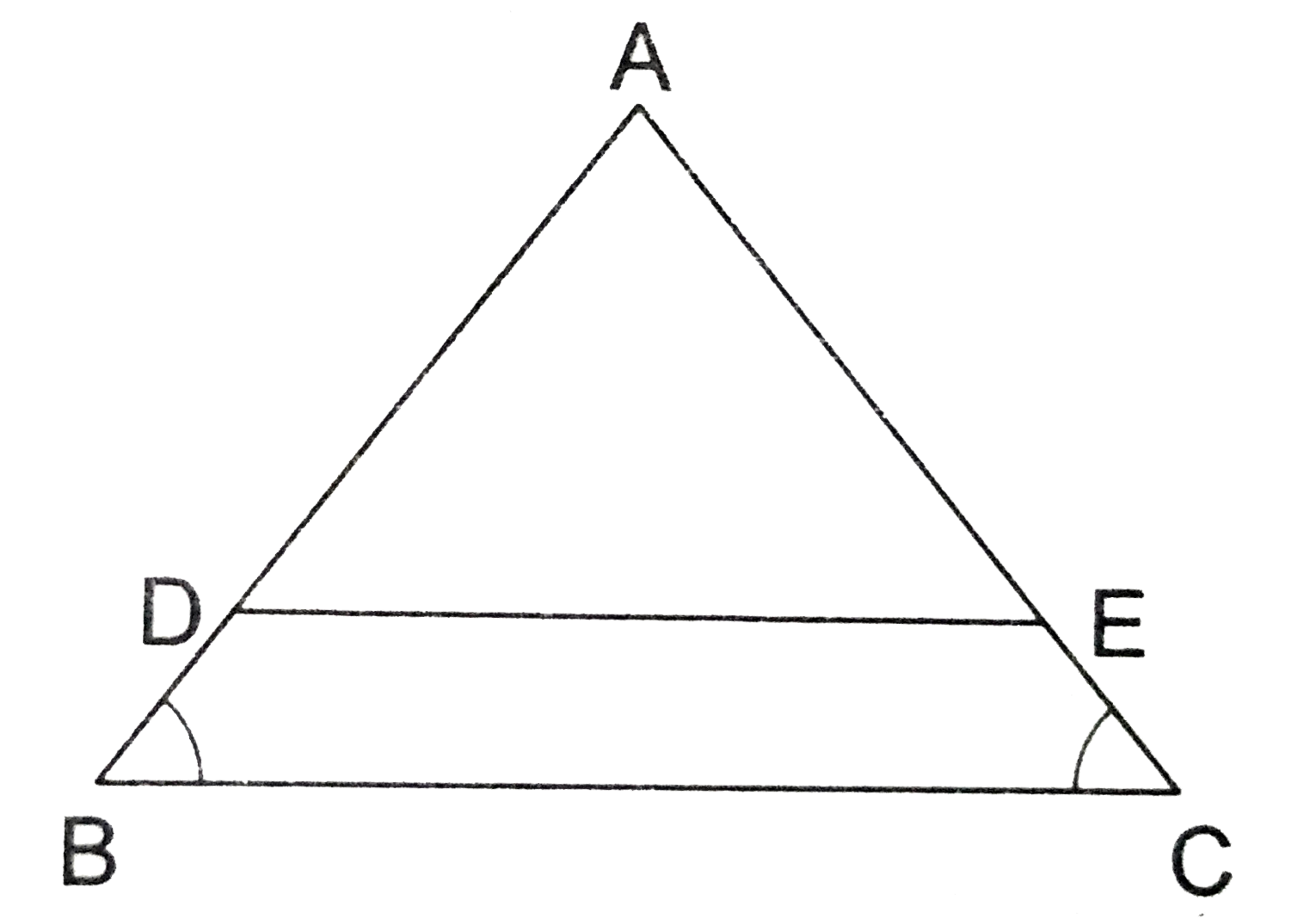
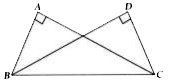
View SolutionIn the given figure, triangles ABC and DCB are right angled at A and D respectively and AC = DB, then prove that ∠ACB = ∠DBC.
View SolutionABC is a triangle right angled at B. D is a point on AC such that ∠ABD=45∘ If AC=6 and AD=2 then AB=
View Solution