In the adjoining figure, AD is a median of ΔABC. If BL and CM are drawn perpendiculars on AD and AD produced, prove that BL = CM.
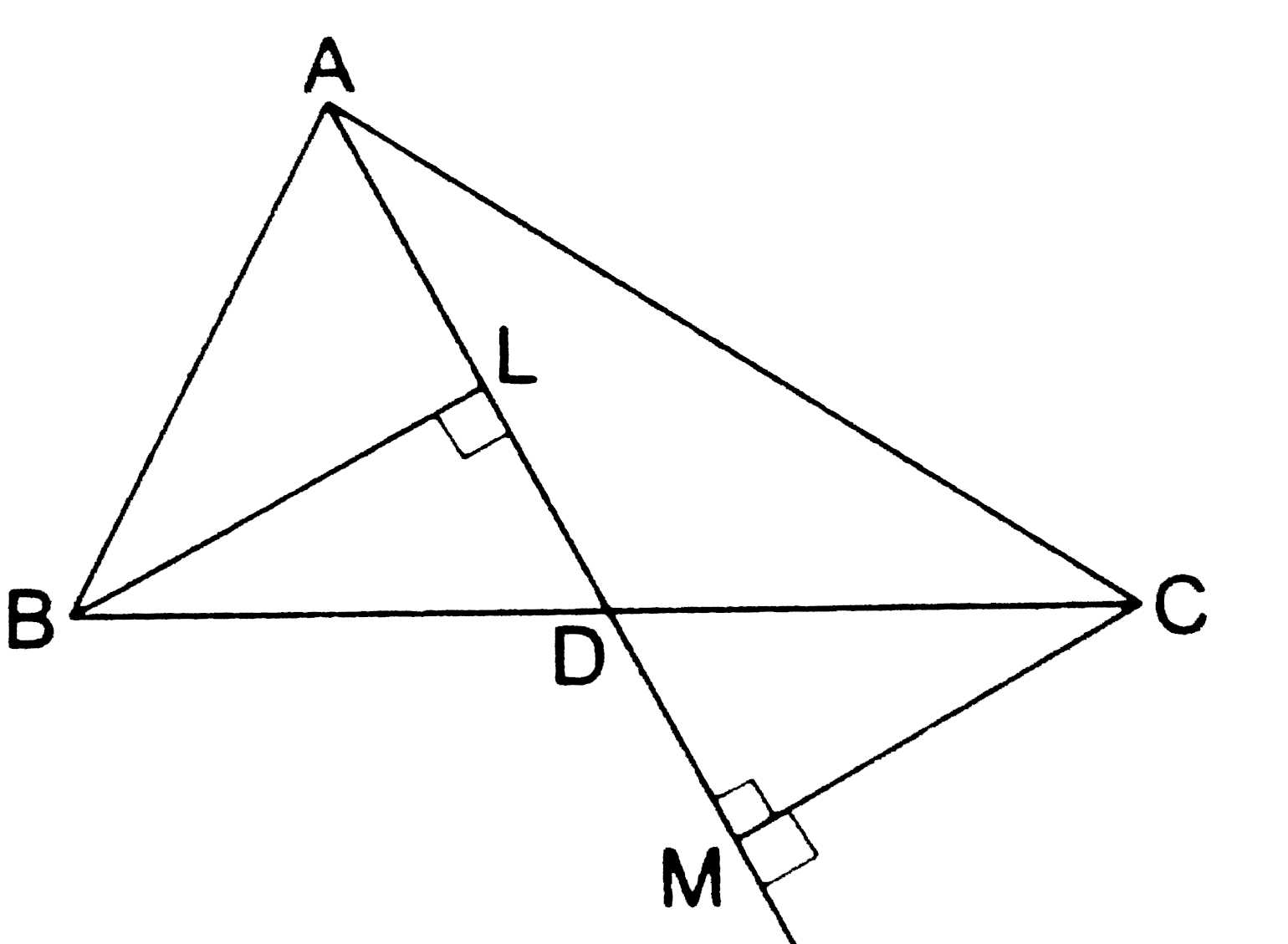
In right triangles ΔBLD and ΔCMD, we have
BD=CD [∵D is the midpoint of BC]
∠BLD=∠CMD [each equal to 90∘]
∠BDL=∠CDM [vert. opp. ∠s]
∴ ΔBLD≅ΔCMD [AAS-criteria].
Hence, BL=CM [c.p.c.t.]
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
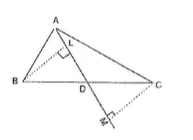
In the adjoining figure, D is the mid-point of BC. If BM and CN are perpendiculars from B and C respectively on AD and AD produced, then prove that BM = CN.

View SolutionIn Figure, AD is a median and BL, CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM
View Solution
Knowledge Check
In the adjoning figure of ΔABC,AD is the perpendicular bisector of side BC. The triangle ABC is :
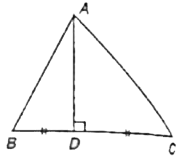 Aright angledBisoscelesCscaleneDequilateral
Aright angledBisoscelesCscaleneDequilateral
In Figure, AD is a median and BL,CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM.

View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)

View SolutionIn △ ABC, AD is a median. Prove that AB + AC > 2AD
View SolutionIn the figure below, AL is perpendicular to BCandCM is perpendicular to AB. If CL=AL=2BL, find MCAM.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is a median.
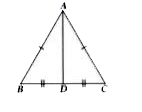 Prove that:
Prove that:
ΔADB≅ΔADC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
AD⊥BC
View Solution
