Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show p=pi'+miV
where pi is the momentum of the ith particle (of mass mi) and p'i=miv'i. Note v'i is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass ∑p'i=O
(b) Show K=K'+1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show L=L'+R×MV
where L'=∑r'i×p'i is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember – r'i=ri−R , rest of the notation is the standard notation used in the chapter. Note ′ L and MR×V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show dL'dt=∑r'i×dp'dt
Further, show that
dL'dt=τ'ext
where τ'ext is the sum of all external torques acting on the system about the centre of mass. Solution in Tamil
Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:NCERT TAMILChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:EXERCISES (TRUE OR FALSE)
Explore 5 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:NCERT TAMILChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:EXERCISES (TRUE OR FALSE)
Explore 5 Videos
- PROPERTIES OF MATTERBook:NCERT TAMILChapter:PROPERTIES OF MATTERExercise:EVALUATION (MULTIPLE CHOICE QUESTIONS)
Explore 14 Videos
- THERMAL PROPERTIME OF MATTERBook:NCERT TAMILChapter:THERMAL PROPERTIME OF MATTERExercise:EXERCISES
Explore 31 Videos
Similar Questions
Read each statement below carefully and state with reasons, if it is true ot false. (a) During rolling the force of friction acts in the same direction as the direction of motion of c.m of the body. (b) The instantaneous speed of the point of contact during rolling is zero. (c ) The instantaneous acceleration of the point of contact during rolling is zero. (d) For perfect rolling motion, work done against friction is zero. (e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling motion).
View SolutionRead each statement below carefully and state with reasons, if it is true ot false. (a) During rolling the force of friction acts in the same direction as the direction of motion of c.m of the body. (b) The instantaneous speed of the point of contact during rolling is zero. (c ) The instantaneous acceleration of the point of contact during rolling is zero. (d) For perfect rolling motion, work done against friction is zero. (e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling motion).
View SolutionConsider two wires X and Y. The radius of wire X is 3 times the radius of Y. If they are stretched by the same load then the stress on Y is
View SolutionThe triple point of neon and carbon dioxide are 24.57K and 216.55K respectively. Express these temperature on the Celsius and Fahrenheit scales.
View SolutionConsider a system of two particles having masses m_(1) and m_(2) . If the particle of mass m_(1) is pushed towards the centre of mass of particles through a distance d , by what distance would the particle of mass m_(2) move so as to keep the mass centre of particles at the original position?
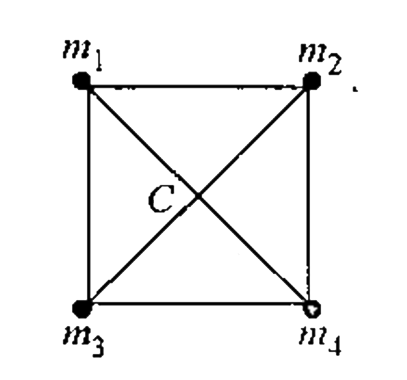
View SolutionFour particle of masses m1=2kg,m2=4kg,m3=1kg and m4 are placed at four corners of a square as shown in figure. Can mass of m4 be adjusted I such a way that the centre of mass of system will be at the centre of the square C.
View SolutionSeparation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass : (a) Show P=P_(i)+m_(i)V where p_(i) is the momentum of the ith particle (of mass m_(i)) and p_(i)=m_(i)v_(t) " Note" v_(i) is the velocity of the ith particle relative to the centre of mass. Also, prove using the definition of the centre of mass sum p_(t)=0 (b) Show K=K'+1//2MV^(2) where K is the total kinetic energy of the system of particles. K' is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV^(2)//2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14. (c ) Show L=L'+RxxMV where L'=sum r'_(t)xxp'_(t) is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember r'_(i)=r_(i)-R , rest of the notation is the standard notation used in the chapter. Note L' and MRxxV can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. (d) Show (dL')/(dt)=sum r'_(i)xx(dp')/(dt) Further, show that (dL')/(dt)=tau'_("ext") where tau_("ext") is the sum of all external torques acting on the system about the centre of mass. (Hint : Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.)
View SolutionThree particles of masses m,m and 4kg are kept at a verticals of triangle ABC. Coordinates of A, B and C are (1,2) , (3,2) and (−2,−2) respectively such that the centre of mass lies at origin. Find the value of mass m.
Hint. xcm=∑3i−1mixi∑3i=1mi, ycm=∑3i=1miyi∑3i=1mi
View SolutionA system of two particles is having masses m_(1) and m_(2) . If the particle of mass m_(1) is pushed towards the centre of mass of particles through a distance d, by what distance the particle of mass m_(2) should be moved so as to keep the centre of mass of particles at the original position ?
View Solutionकणों के किसी निकाय की गति को इसके द्रव्यमान केंद्र की गति और द्रव्यमान केंद्र के पारित : गति में अलग - अलग विचार करके दर्शाइए कि-
(a) →p=−→p'i+M→V, जहाँ →pi (mi द्रव्यमान वाले ) i - वें कण का संवेग है, और −→p'i=mi−→v'i| ध्यान दें कि −→v'i द्रव्यमान केंद्र के सापेक्ष i- वें कण का वेग है । द्रव्यमान केंद्र की परिभाषा का उपयोग करके यह भी सिद्ध कीजिए कि Σ−→p'i=0.
View SolutionSeparation of motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
(a)n Show →p=→pi+mi→V where →pi is the momentum of the ith particle (of mass mi) and →pi=mi→vi, Not →vi is the velocity of the ith particle relative to the centre ofmass.
Also, prove using the definition of the centre of mass ∑→pi=0
(b) Show K=K'+1/2MV2 where K is the total kinetic energy of the system of particles, K is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system)
(c) Show →L=→L+→R×MV
where →L'=∑→ri×→pi is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember →ri=→ri−→R, reat of the notation is the standard notation used in the chapter. Note →L'andM→R×→V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show d→Ldt=∑→ri×d→p'dt Further show that d→L'dt=→τext' where Text is the sum of all external torques acting on the system about the centre of mass. (Hint: Use the definition of centre of mass and Newton's Third Law. Assume the internal forces between any two particles aet along the line joining the particles.)
View SolutionSeparation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show p=pi'+miV
where pi is the momentum of the ith particle (of mass mi) and p'i=miv'i. Note v'i is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass ∑p'i=O
(b) Show K=K'+1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show L=L'+R×MV
where L'=∑r'i×p'i is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember – r'i=ri−R , rest of the notation is the standard notation used in the chapter. Note ′ L and MR×V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show dL'dt=∑r'i×dp'dt
Further, show that
dL'dt=τ'ext
where τ'ext is the sum of all external torques acting on the system about the centre of mass.
View SolutionSeparation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show p=pi'+miV
where pi is the momentum of the ith particle (of mass mi) and p'i=miv'i. Note v'i is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass ∑p'i=O
(b) Show K=K'+1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show L=L'+R×MV
where L'=∑r'i×p'i is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember – r'i=ri−R , rest of the notation is the standard notation used in the chapter. Note ′ L and MR×V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show dL'dt=∑r'i×dp'dt
Further, show that
dL'dt=τ'ext
where τ'ext is the sum of all external torques acting on the system about the centre of mass.
View SolutionSeparation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show p=pi'+miV
where pi is the momentum of the ith particle (of mass mi) and p'i=miv'i. Note v'i is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass ∑p'i=O
(b) Show K=K'+1/2MV2
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV2/2 is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show L=L'+R×MV
where L'=∑r'i×p'i is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember – r'i=ri−R , rest of the notation is the standard notation used in the chapter. Note ′ L and MR×V can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show dL'dt=∑r'i×dp'dt
Further, show that
dL'dt=τ'ext
where τ'ext is the sum of all external torques acting on the system about the centre of mass.
View SolutionSeparation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass : (a) Show p=p_(i).+m_(i)V where p_(i) is the momentum of the ith particle (of mass m_(i) ) and p_(i).=m_(i)v_(i). . Note v_(i). is the velocity of the i^(th) particle relative to the centre of mass Also, prove using the definition of the centre of mass Sigmap_(i).=0 (b) Show K=K.+(1)/(2)MV^(2) where K is the total kinetic energy of the system of particles, K. is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and (1)/(2)MV^(2) is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14). (c ) Show vecL=vecL.+vecRxxvec(MV) where vecL.=Sigmavec(r_(i)).xxvec(p_(i)). is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember vec(r._(i))=vec(r_(i))-vecR , rest of the notation is the velcities taken relative to the centre of mass. Remember vec(r._(i))=vec(r_(i))-vecR rest of the notation is the standard notation used in the chapter. Note vecL , and vec(MR)xxvecV can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. (d) Show vec(dL.)/(dt)=sumvec(r_(i).)xxvec(dp.)/(dt) Further, show that vec(dL.)/(dt)=tau._(ext) where tau._(ext) is the sum of all external torques acting on the system about the centre of mass. (Hint : Use the definition of centre of mass and Newton.s Thrid Law. Assume the internal forces between any two particles act along the line joining the particles.)
View Solution

