If tangents are drawn to the ellipse $x^{2} + 2 y^{2} = 2,$ then the locus of the midpoint of the intercept made by the tangents between the coordinate axes is $\frac{1}{2 x^{2}} + \frac{1}{4 y^{2}} = 1$ (b) $\frac{1}{4 x^{2}} + \frac{1}{2 y^{2}} = 1$ $\frac{x^{2}}{2} + y^{2} = 1$ (d) $\frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$

$\frac{1}{2 x^{2}} + \frac{1}{4 y^{2}} = 1$

$\frac{1}{4 x^{2}} + \frac{1}{2 y^{2}} = 1$

$\frac{x^{2}}{2} + \frac{y^{2}}{4} = 1$

$\frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$

Video Solution

Text Solution

Verified by Experts

Any tangent to ellipse
$\frac{x^{2}}{4} + \frac{y^{2}}{1} = 1$ is given by
$\frac{x cos θ}{\sqrt{2}} + y sin θ = 1$

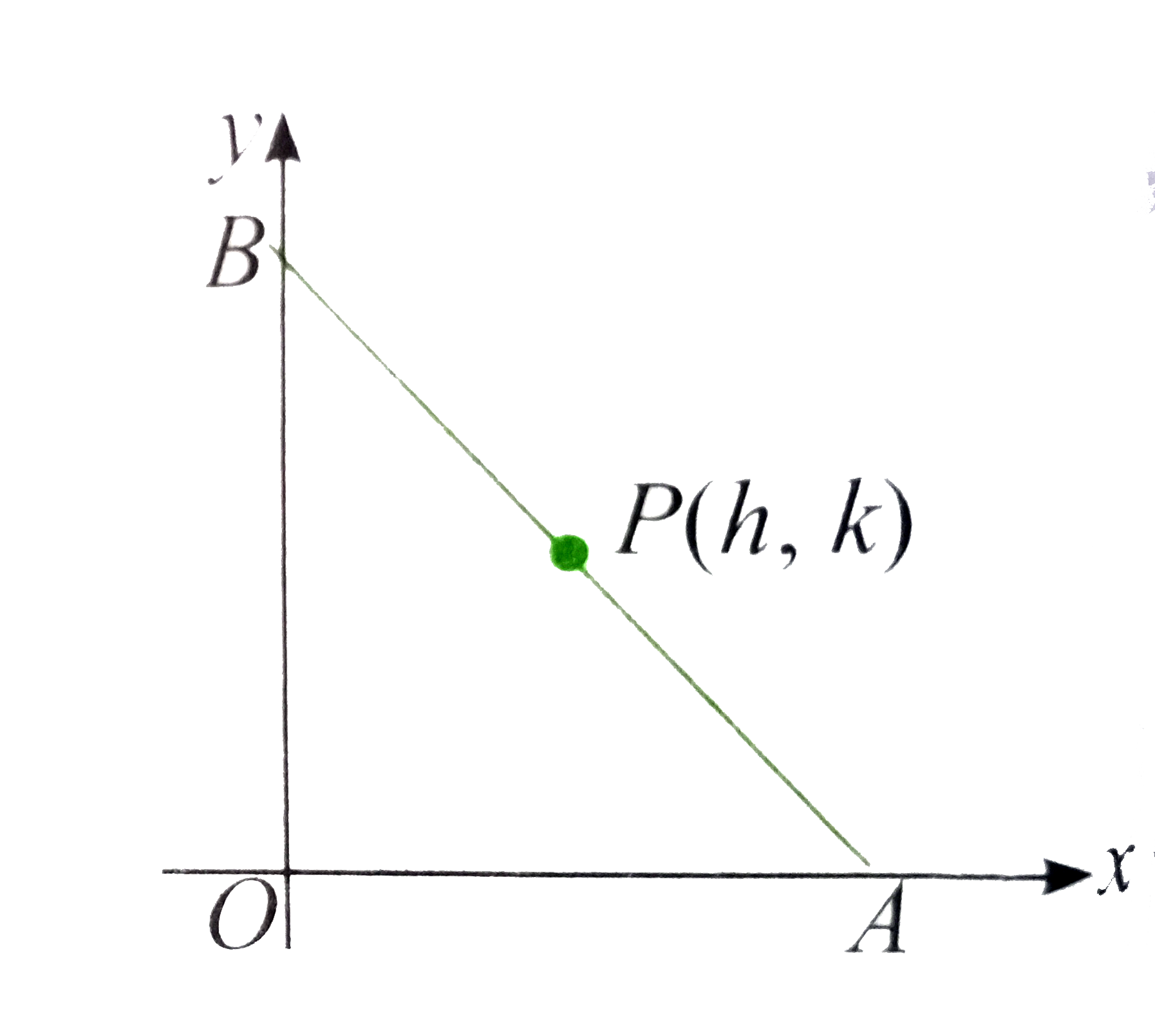
Let it meet axes at A and B
$∴ A \equiv (\sqrt{2} sec θ, 0) and B \equiv (0, coses θ)$
Let p(h,k) be the mid point of AB.
Hence, $2 h = \sqrt{2} sec θ$ and $2 k = cosec$ which is locus of P
${(\frac{1}{\sqrt{2} h})}^{2} + {(\frac{1}{2 k})}^{2} = 1$

$or \frac{1}{2 h^{2}} + \frac{1}{4 k^{2}} = 1$
$or \frac{1}{2 x^{2}} + \frac{1}{4 y^{2}} = 1$

Updated on:21/07/2023

If tangents are drawn to the ellipse $x^{2} + 2 y^{2} = 2,$ then the locus of the midpoint of the intercept made by the tangents between the coordinate axes is $\frac{1}{2 x^{2}} + \frac{1}{4 y^{2}} = 1$ (b) $\frac{1}{4 x^{2}} + \frac{1}{2 y^{2}} = 1$ $\frac{x^{2}}{2} + y^{2} = 1$ (d) $\frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$
A $x^{2} + 2 y^{2} = 4 x^{2} y^{2}$
B $2 x^{2} + y^{2} = 4 x^{2} y^{2}$
C $2 x^{2} + y^{2} = 4$
D $x^{2} + 2 y^{2} = 4$
Tangents are drawn to $x^{2} + 3 y^{2} = 2$ . The locus" of mid-point of intercept made by tangents between the axes is
A $\frac{1}{x^{2}} + \frac{1}{2 y^{2}} = 1$
B $\frac{1}{4 x^{2}} + \frac{1}{2 y^{2}} = 1$
C $\frac{1}{2 x^{2}} + \frac{1}{6 y^{2}} = 1$
D $\frac{1}{2 x^{2}} + \frac{1}{y^{2}} = 1$
Find the locus of mid-point of the portion of tangent intercepted between coordinate axes to the circle $x^{2} + y^{2} = 1$ .
A $x^{2} + y^{2} - 4 x^{2} y^{2} = 0$
B $x^{2} + y^{2} - 2 x y = 0$
C $x^{2} + y^{2} - 2 x^{2} Y^{2} = 0$
D $x^{2} y^{2} = 0$