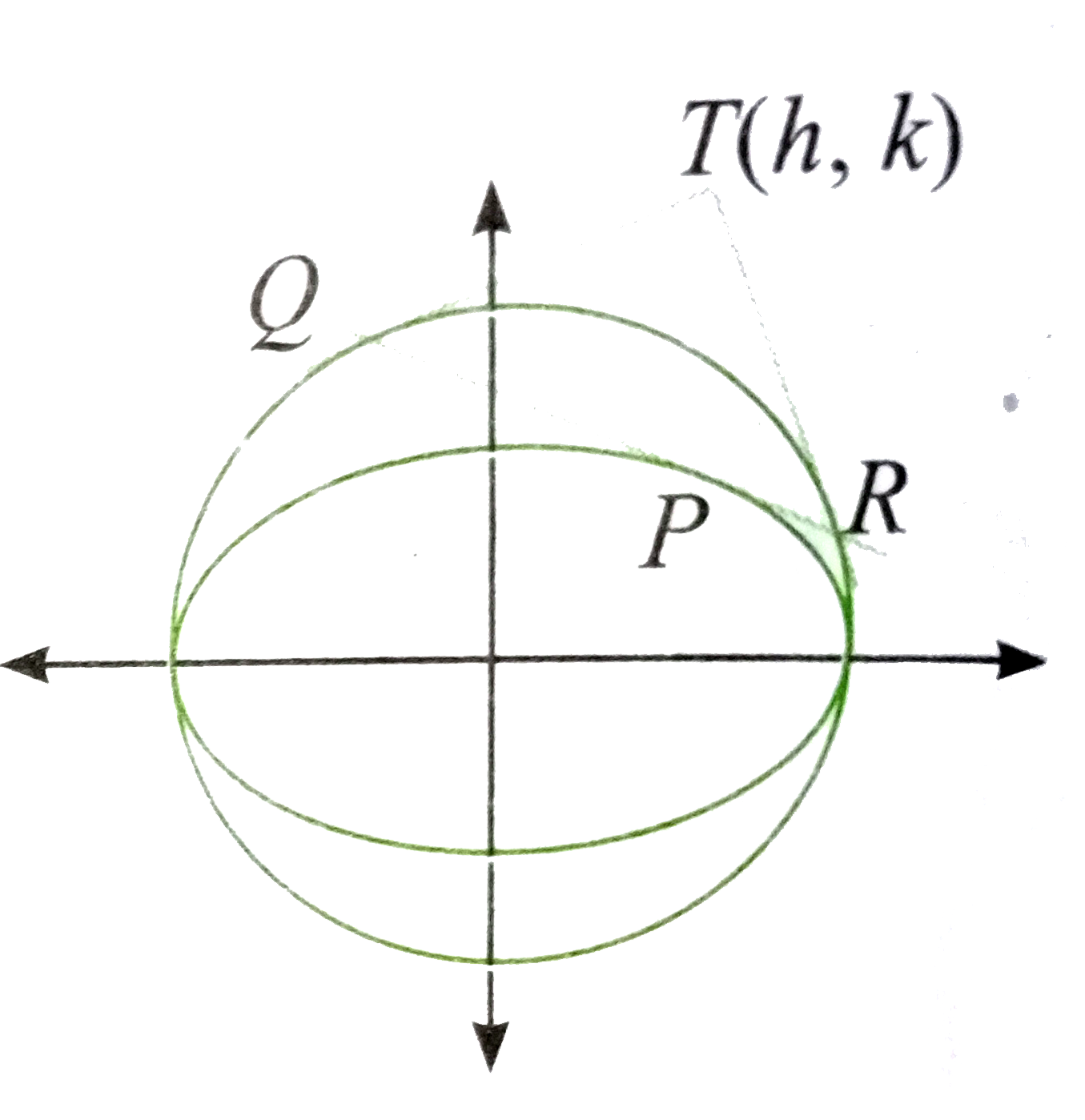
If the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
The correct Answer is:(1,√2,1)
The equation of tangent to the ellipse at a given points is x(1√2)+2y(12)=1
or x+√y=√2 (1)
Now, QR is the chord of contact of the circle x2_y2=1 with respect to the point T(h,k). Then,
QR≡hx+ky+ky=1 (2)
Equations (1) and (2) represent the same straight line. Then comapring the ratio of coefficients, we have, h/1=k/√2=1√2.
Hence (h,k)≡(1/√2)
Similar Questions
If the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View SolutionIf the tangents are drawn to the circle x2+y2=12 at the point where it meets the circle x2+y2−5x+3y−2=0, then find the point of intersection of these tangents.
View Solution
Knowledge Check
If the tangents are drawn to the circle x2+y2=12 at the point where it meets the circle x2+y2−5x+3y−2=0, then the point of intersection of these tangents is
A(6, -6)B(6,18/5)C(6,−18/5)Dnone of theseTangents are drawn to the circle x2+y2=16 at the points where it intersects the circle x2+y2−6x−8y−8=0, then the point of intersection of these tangents is
A(4,163)B(12,16)C(3,4)D(16,12)
A variable tangent to the circle x2+y2=1 intersects the ellipse x24+y22=1 at point P and Q. The lous of the point of the intersection of tangents to the ellipse at P and Q is another ellipse. Then find its eccentricity.
View SolutionIf the tangent at θ on the ellipse x2a2+y2b2=1 meets the auxiliary circle at two points which subtend a right angle at the centre,then e2(2−cos2θ)=
View SolutionIf the tangent at θ on the ellipse x2a2+y2b2=1 meets the auxiliary circle at two points which subtend a right angle at the centre then e2(2−cos2θ)=
View SolutionIf the straight line x−2y+1=0 intersects the circle x2+y2=25 at points P and Q, then find the coordinates of the point of intersection of the tangents drawn at P and Q to the circle x2+y2=25.
View Solutionif a variable tangent of the circle x2+y2=1 intersects the ellipse x2+2y2=4 at P and Q. then the locus of the points of intersection of the tangents at P and Q is
View SolutionLocus of point of intersection of perpendicular tangents to the circle x2+y2−4x−6y−1=0 is
View Solution
