Question

If the area of the ellipse ${\displaystyle \left(\frac{x^2}{a^2}\right)+\left(\frac{y^2}{b^2}\right)=1}$
is ${\displaystyle 4\pi }$
, then find the maximum area of rectangle
inscribed in the ellipse.

Answer

8 sq. units

Explanation

The area of ellipse `(x^(2)//a^(2))+(y^(2)//b^(2))=1 "is" piab=4pi` (given) . Therefore, ab=4
`A(a cos theta, b sin theta)`
on the ellipse.
Now, the area of reactangle ABCD inscribed in the ellipse is

`Delta=4(a cos theta)(b sin theta)`
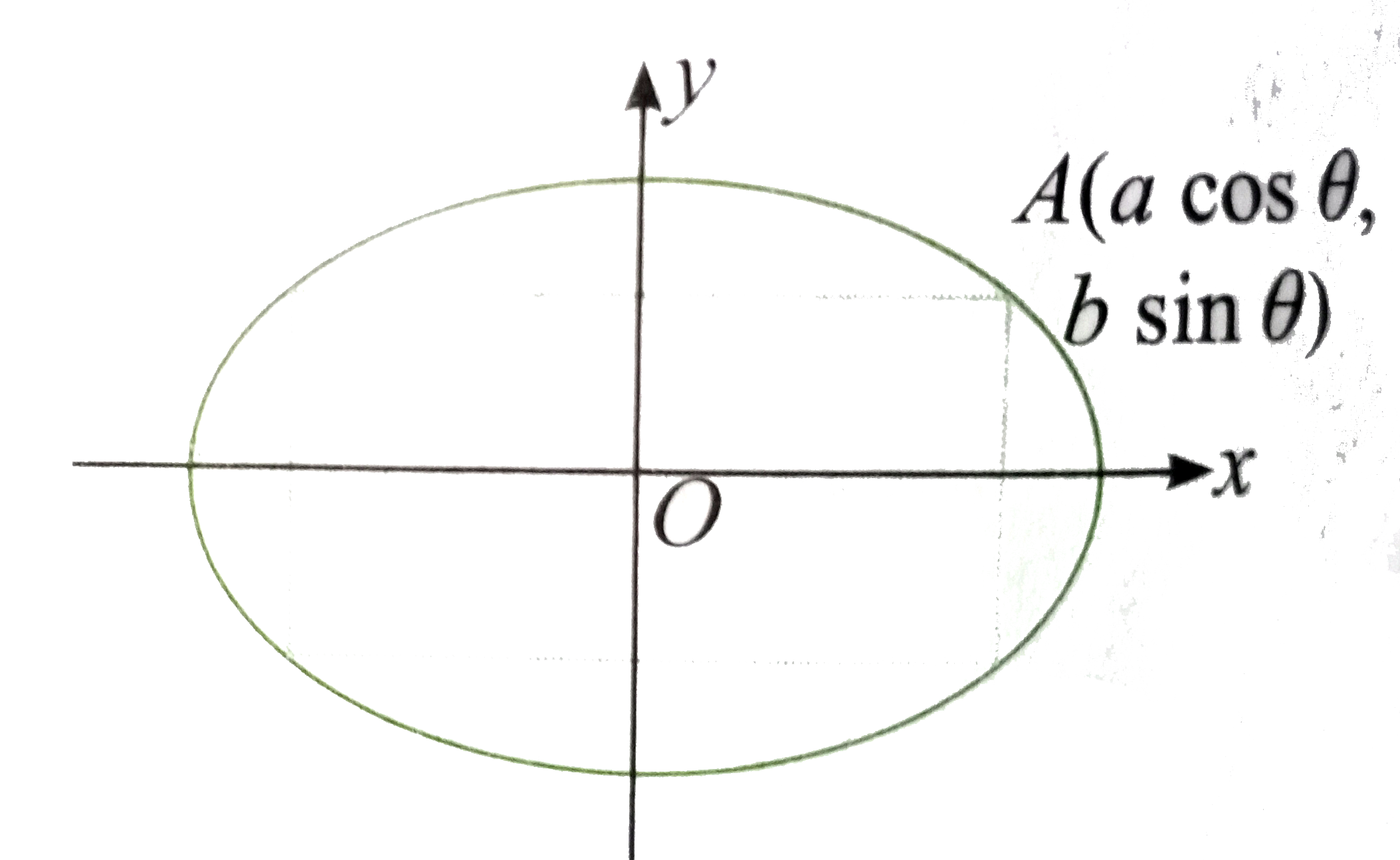
or `Delta=2absin 2 theta`
`:. Delta_("max")=2ab=8`