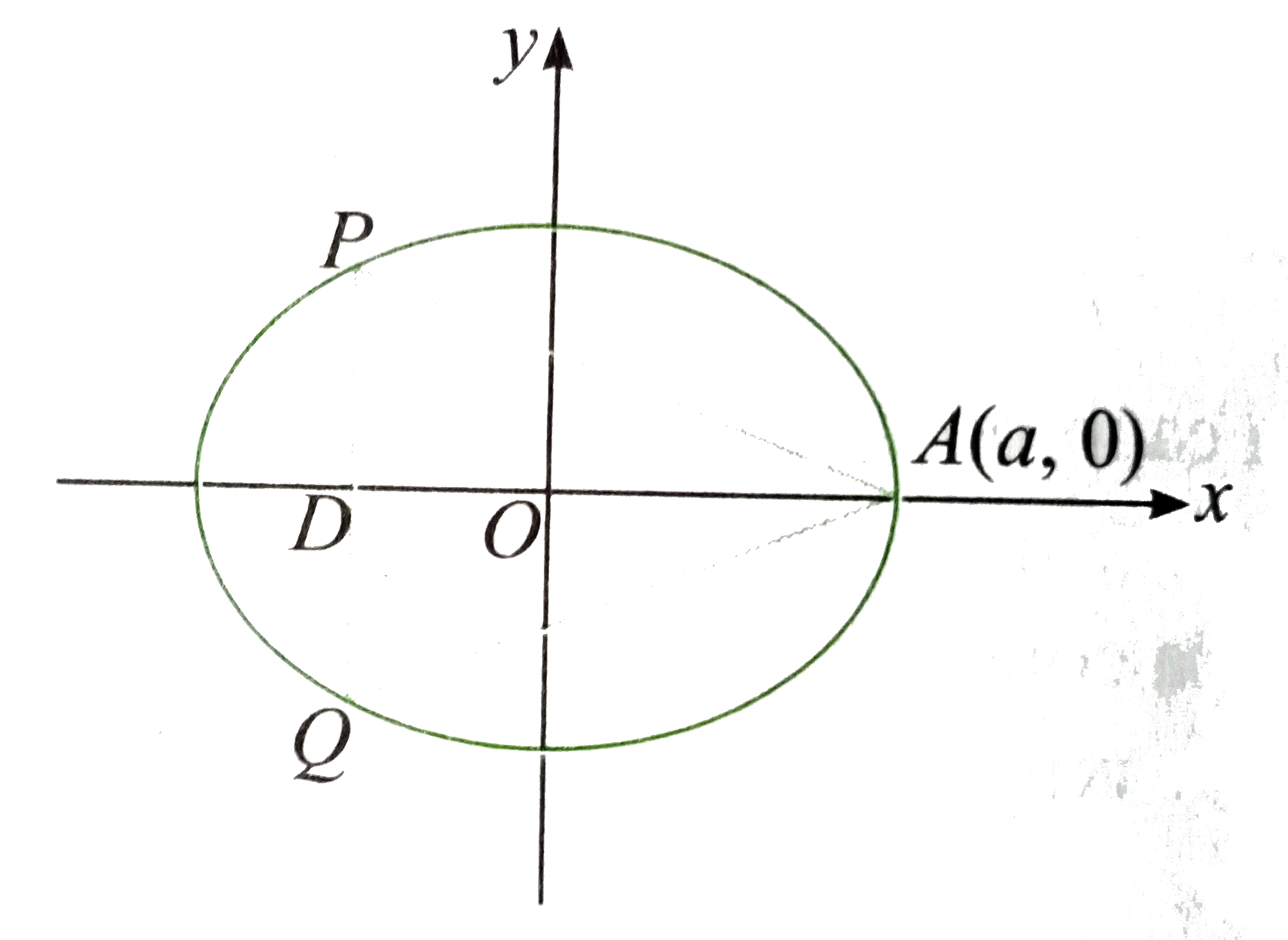
Find the area of the greatest isosceles triangle that can be inscribed in the ellipse $(\frac{x^{2}}{a^{2}}) + (\frac{y^{2}}{b^{2}}) = 1$ having its vertex coincident with one extremity of the major axis.

Video Solution

Text Solution

Verified by Experts

Let APQ be the isoceles triangle inscribed in the ellipse $(x^{2} / a^{2}) + (y^{2} / b^{2}) = 1$ with one vertex A at the extermity (a,0) of the major axis. If the coordinates of P are $(a cos θ, - b sin θ)$ then those of Q will be $(a cos θ b - sin θ)$ ,
So, area of $Δ A P Q$ . is given by
$Δ = \frac{1}{2} P Q \cdot A D$
$= P D \cdot A D$
$= P D (O A + O D)$
$= b sin θ (a - a cos θ)$
$= \frac{1}{2} a b (2 sin θ - sin 2 θ), 0 < θ \leq π$

$∴ \frac{d Δ}{Δ θ} = a b (cos θ - cos 2 θ)$
and $\frac{d^{2} Δ}{d θ^{2}} = a b (- sin θ + 2 sin 2 θ)$
For maximum or minimum of $Δ$ .
$\frac{d Δ}{d θ} = 0$
$or cos θ - cos 2 θ = 0$
$or 2 {cos}^{2} θ - cos θ - 1 = 0$
or $(2 cos θ + 1) (cos θ - 1) = 0$
$or cos θ = \frac{1}{2} (∴ cos θ \neq 1 a s θ \neq 0)$
or $θ = \frac{2 π}{3}$
Whern $θ = 2 π / 3$ , we have
$\frac{d^{2} Δ}{d θ^{2}} = - \frac{1}{2} (3 \sqrt{3}) a b, (- v e)$
Therfore the area is maximum when $θ = 2 π / 3$
Therefore, maximum area
$Δ = \frac{1}{2} a b [2 sin . \frac{2 π}{3} - sin . \frac{4 π}{3}]$
$= \frac{1}{4} (3 \sqrt{3}) a b$

Updated on:21/07/2023

The sides of the greatest rectangle that can be inscribed in the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ are
A $a \sqrt{2}, b \sqrt{2}$
B $\sqrt{a}, \sqrt{b}$
Ca,b
D $\frac{a}{\sqrt{2}}, \frac{b}{\sqrt{2}}$
Find the area of the greatest rectangle that can be inscribed in an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
A $\sqrt{a b}$
B $a / b$
C $2 a b$
D $a b$