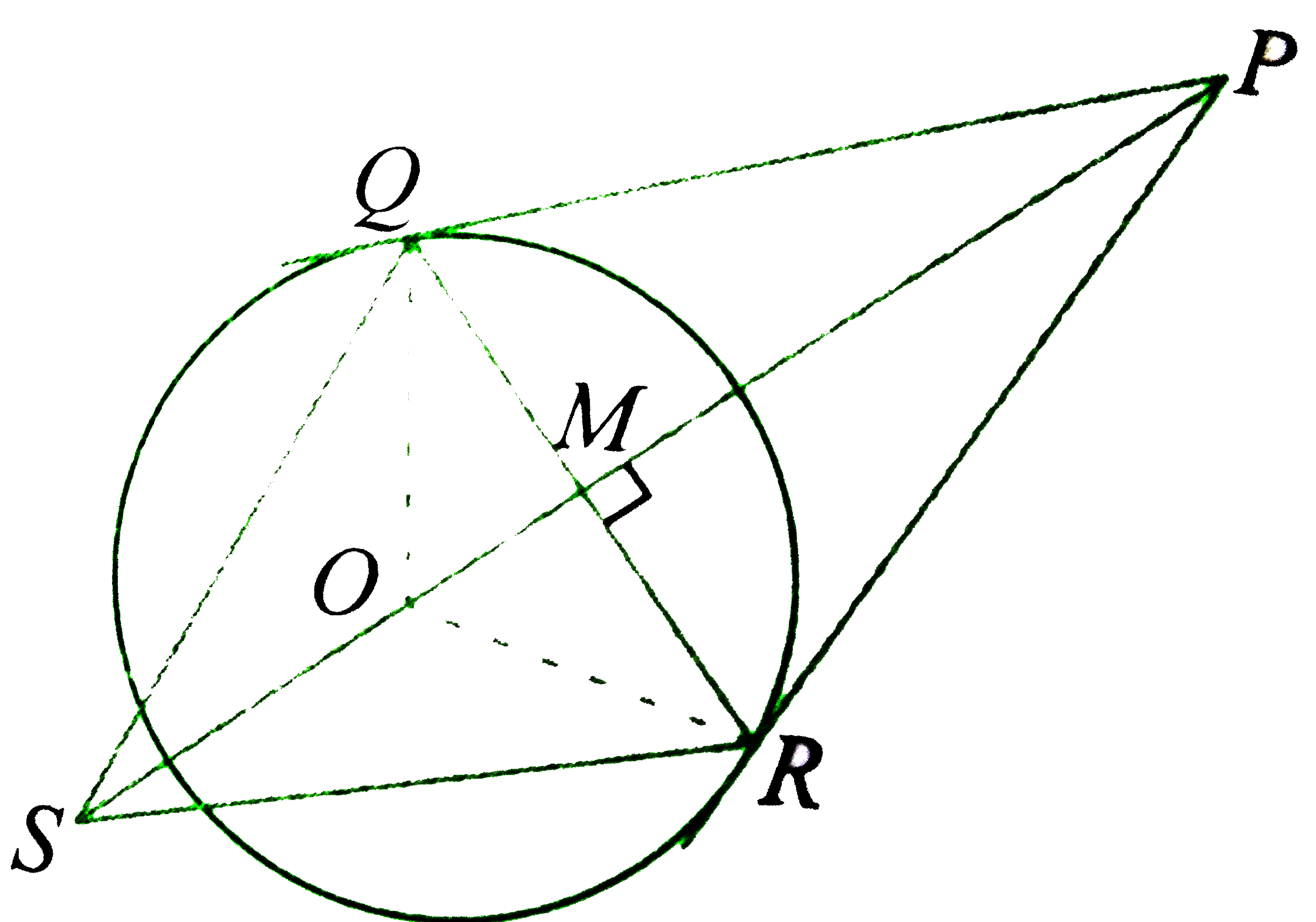
P is a variable point of the line L = 0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed. If L=2x+y−6=0, then the locus of circumcetre of △PQR is -
2x−y=4
2x+y=3
x−2y=4
x+2y=3
The correct Answer is:2
PQ=PR, i.e., paralleleogram PQSR is a rhombus. Therefore,
Midpoint of QR= Midpoint of PS and QR⊥PS
Therefore , S is the mirror image of P in QR
L≡2x+y−6
Let P≡(k,6−2k) .
∠PQO=∠PRO=π2
Therefore, OP is the diameter of circumsircle PQR. Then the center is (k/2,3−k) . So,
x=k2 or k=2x and y=3−k
Therefore, the required locus is 2x+y=3
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
P is a variable point of the line L = 0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed. If L=2x+y−6=0, then the locus of circumcetre of △PQR is -
View SolutionP is a variable point on the line L=0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogran PQSR is completed.
If P-=(6,8) then area of ΔQRS is 19225√λ sq units. The value of λ is
View Solution
Knowledge Check
P is a variable point on the line L=0 . Tangents are drawn to the circles x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed.
If P≡(3,4), then the coordinates of S areA(−46/25,63/25)B(−51/25,−68/25)C(−46/25,68/25)D(−68/25,51/25)P is a variable point on the line L=0 . Tangents are drawn to the circles x2+y2=4 from P to touch it at Q and R. The parallelogram PQSR is completed.
If P≡(6,8), then the area of ΔQRS isA3√625 sq. unitsB3√2425 sq. unitsC48√625 sq. unitsD192√625 sq. unitsP is a variable point on the line L=0. Tangents are drawn to the circle x2+y2=4 from P to touch it at Q and R. The parallelogran PQSR is completed.
If p-=(3,4), then the coordinates of S areA(−46/25,63/25)B(−51/25,−68/25)C(−46/25,68/25)D(−68/25,51/25)
P is variable point on the line y=4. tangents are drawn to the circle x2+y2=4 from the points touch it at A and B. The parallelogram PAQB be completed.If locus of Q is (y+a)(x2+y2)=by2 ,the value of a+b Is:
View SolutionFrom a variable point R on the line y = 2x + 3 tangents are drawn to the parabola y2=4ax touch it at P and Q point. Find the locus of the centroid of the triangle PQR.
View SolutionLet P be a variable point. From P tangents PQ and PR are drawn to the circle x2+y2=b2 if QR always touch the parabola y2=4ax then locus ofP is
View Solutionif P is a variable point and PQ and PRare the tangent drawn to the circle x2+y2=9. Let QR be always touching the circle x+y2=4, then locus of P is
View SolutionA circle touching the line x+y−2=0 at (1,1) and cuts the circle x2+y2+4x+5y−6=0 at P and Q. Then
View Solution
