Consider the following four force vectors:
→F1=50.0N, due east, →F2=10.0N, due east,
→F3=40.0N, due west,→F4=30.0N, due west
Which two vectors add together to give a resultant with smallest magnitude ? In the option below, the two vectors are given followed by a magnitude and direction.
→F1+→F3,10−N, due east
→F1+→F3,10N, due east
→F1+→F2,20N due east
→F1+→F4,20N due west
The correct Answer is:A
To solve the problem of which two force vectors add together to give a resultant with the smallest magnitude, we will follow these steps:
Step 1: Identify the Force Vectors
We have the following force vectors:
- →F1=50.0N (due east)
- →F2=10.0N (due east)
- →F3=40.0N (due west)
- →F4=30.0N (due west)
Step 2: Assign Directions
We can represent east as positive and west as negative. Thus:
- →F1=+50.0N
- →F2=+10.0N
- →F3=−40.0N
- →F4=−30.0N
Step 3: Calculate Resultants for Each Pair
We will calculate the resultant for each possible pair of vectors:
1. Pair →F1 and →F2:
R12=→F1+→F2=50.0+10.0=60.0N(east)
2. Pair →F1 and →F3:
R13=→F1+→F3=50.0−40.0=10.0N(east)
3. Pair →F1 and →F4:
R14=→F1+→F4=50.0−30.0=20.0N(east)
4. Pair →F2 and →F3:
R23=→F2+→F3=10.0−40.0=−30.0N(west)
5. Pair →F2 and →F4:
R24=→F2+→F4=10.0−30.0=−20.0N(west)
6. Pair →F3 and →F4:
R34=→F3+→F4=−40.0−30.0=−70.0N(west)
Step 4: Compare Resultant Magnitudes
Now we compare the magnitudes of the resultant vectors:
- |R12|=60.0N
- |R13|=10.0N
- |R14|=20.0N
- |R23|=30.0N
- |R24|=20.0N
- |R34|=70.0N
The smallest magnitude is 10.0N from the pair →F1 and →F3.
Conclusion
The two vectors that add together to give a resultant with the smallest magnitude are:
- →F1 and →F3
- Resultant magnitude: 10.0N (due east)
---
We have the following force vectors:
- →F1=50.0N (due east)
- →F2=10.0N (due east)
- →F3=40.0N (due west)
- →F4=30.0N (due west)
We can represent east as positive and west as negative. Thus:
- →F1=+50.0N
- →F2=+10.0N
- →F3=−40.0N
- →F4=−30.0N
We will calculate the resultant for each possible pair of vectors:
R12=→F1+→F2=50.0+10.0=60.0N(east)
R13=→F1+→F3=50.0−40.0=10.0N(east)
R14=→F1+→F4=50.0−30.0=20.0N(east)
R23=→F2+→F3=10.0−40.0=−30.0N(west)
R24=→F2+→F4=10.0−30.0=−20.0N(west)
R34=→F3+→F4=−40.0−30.0=−70.0N(west)
Now we compare the magnitudes of the resultant vectors:
- |R12|=60.0N
- |R13|=10.0N
- |R14|=20.0N
- |R23|=30.0N
- |R24|=20.0N
- |R34|=70.0N
The two vectors that add together to give a resultant with the smallest magnitude are:
- →F1 and →F3
- Resultant magnitude: 10.0N (due east)
Topper's Solved these Questions
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PROBLEMS
34 Videos
- UNITS AND MEASUREMENT BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
11 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
Similar Questions
Knowledge Check
Two forces →F1=500N due east and →F2=250N due north have their common initial point. →F2−→F1 is
A250√5N,tan−1(2)WofNB250N,tan−1(2)W of NCZeroD750N,tan−1(3/4)NofWThe four pairs of force vectors are given, which pairs of force vectors cannot be added to give a resultant vector of magnitude 10N ?
A2N,13NB5N,16NC7N,8ND100N,105NFind the resultant of the following two vector →A and →B.
→A:40 units due east and , →B:25 units 37∘ north of westA25 units 37∘ north of westB25 units 37∘ north of eastC40 units 53∘ north of westD40 units 53∘ north of east
Four forces are acting on a particle simultaneously : 50N due east , 40 N due north , 30 N due west and 20 N due south . Calculate the resultant force on the particle .
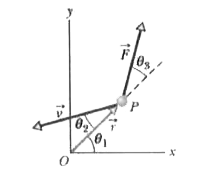
View SolutionAt the instant of Figure, a 2.0 kg particle P has a position vector →r of magnitude 5.0 m and angle θ1=45∘ and a velocity vector →v of magnitude 4.0 m/s and angle θ2=30∘, Force →F, of magnitude 2.0 N and angle θ3=30∘, acts on P. All three vectors lie in the xy plane. About the origin, what are the (a) magnitude and (b) direction of the angular momentum of P and the ( c) magnitude and (d) direction of the torque acting on P?
View SolutionA resultant of 60 N is produced due to two forces having magnitudes in the ratio 4:5 Calculate the magnitude of each if the angle between them is 30∘
View SolutionConsider two vectors →F1=2ˆi+5ˆk and →F2=3ˆj+4ˆk. The magnitude to thhe scalar product of these vectors is
View SolutionTwo forces are applied to a 5.0 kg crate, one is 6.0N to the north and the other is 8.0N to the west. The magnitude of the acceleration of the crate is :
View Solution
