Question

Solve the following problem graphically :
Minimise and Maximise $Z=3x+9y$ . . . (1)
subject to the constraints: $x+3y\le 60$ . . . (2)
$x+y\ge 10$ . . . (3)
$x\le y$ . . . (4)
$x\ge 0,y\ge 0$ . . . (5)

Explanation

Region represented by `x+3yle60`
Consider the equation `x+3y=60.`
`x=0implies 3y=60impliesy=20,y=0impliesx=60`
Plot the points `A(2,20) and B(60,0).` Join AB and produce it both ways.
Putting `x=0 and y=0.` we get `0+3xx0=0le60.`
`thereforeO(0,0)` line in the region `x+3yle60.`
So, the region containing the origin is the solution set of `x+3y ge60.`
Region represented by `x+yge10`
Consider the equation `x+y=10.`
Plot the points `C(0,10) and D(10,0)` Join CD and porducte it both ways.
Now, `x=0, y=0 implies 0+0ge10` is not true.
`therefore O(0,0)` lies in the region `x-y le0.`
We know that:
`x ge0` is the y-axis and the region on its RHS.
`yge0` is the x-axis and the region above the x-axis.
On solving `x=y and x+y=10,` we get the point G(5,5).
On solving `x=yand x+3y=60,` we get `H(15,15).`
Thus, the feasible region is ACGH, as shown in the figure.

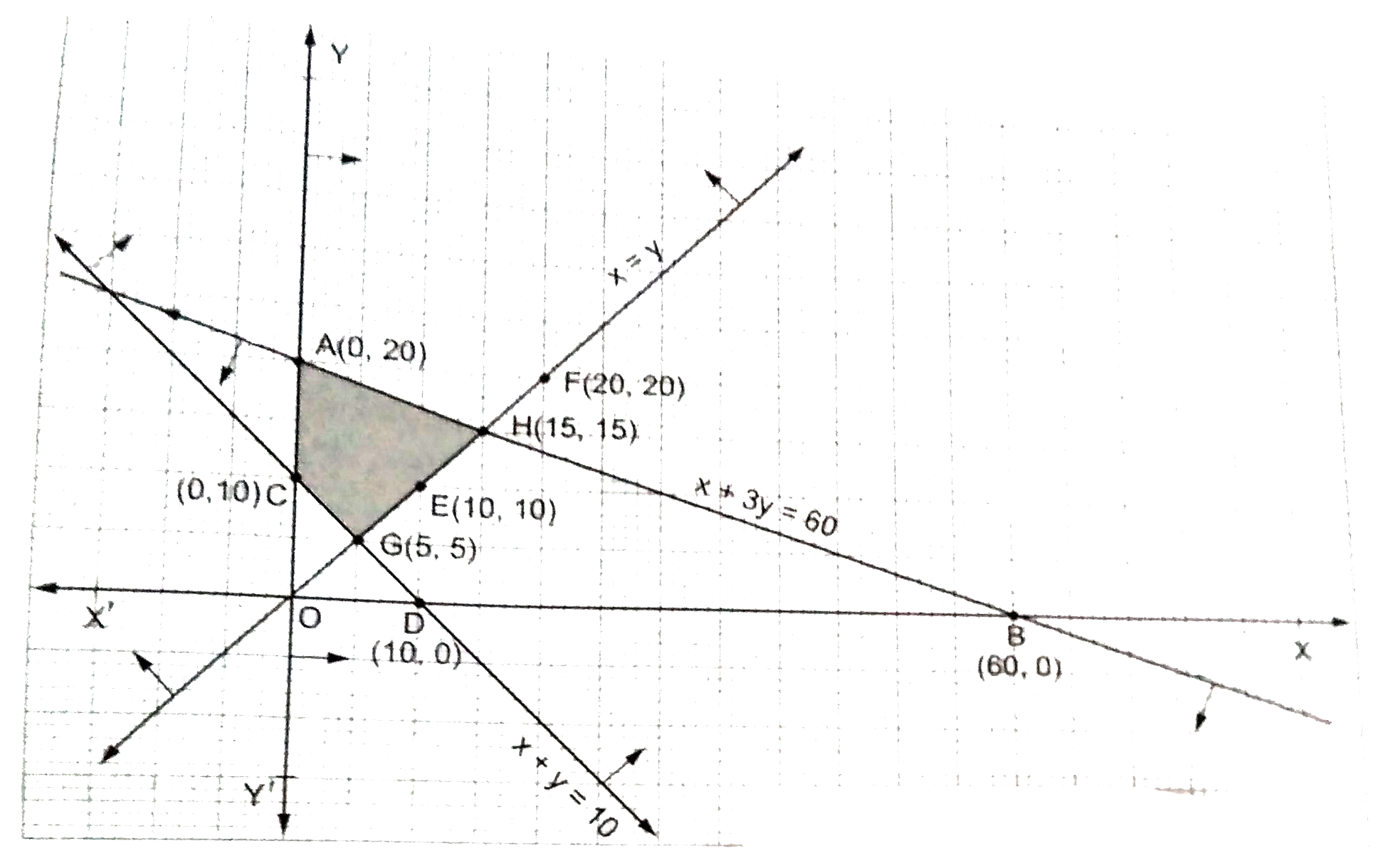
Value of `z=3x+9y:`
`(i) At A(0,20)it is (3xx0+9xx20)=180.`
`(ii) AtC(0,10) "it is"(3xx0+9xx10)=90.`
`(iii) At C(5,5)"it is" (3xx5+9xx10)=60.`
`(iii) At H(15,15)"it is" (3xx15+9xx15)=180.`
So the minimum vlaue of z is 60 and its maximum value is 180.