वायु का एक बुलबुला जिसका आयतन 1.0cm3 है। 40m गहरी झील की तली से जहां ताप12∘C है। उठकर ऊपर पृष्ठ पर आता है। जहां 35∘C है। अब इसका आयतन क्या होगा?
V1=1सेमी3=1×10−6मी3
T1=12∘C=12+273=285 केल्विन
तथा h1=40मी, अतः P1=P0+h1ρg
जहां P0= सतह पर दाब=1 वायुमंडलीय
=1.013×105न्यूटन/मी.2
ρ= जल का घनत्व =103किग्रा./मी03
अतः P1=13.013×105+(40×103×9.8)
P1=4.933×105न्यूटन/मी2
सतह पर आने पर
T2=35∘C=35+273=308 केल्विन
P2=P0=1.013×105न्यूटन/मी2
अतः P1V1T1=P2V2T2
से V2=P1V1T2P2T1
=4.933×105×1×10−6×3081.013×105×285
या V2=5.263×10−6मी3
Topper's Solved these Questions
- अणुगति सिद्धांतBOOK - SCIENCE PUBLICATIONCHAPTER - अणुगति सिद्धांतEXERCISE - NCERT TEXT BOOK PROBLEMS अतिरिक्त अभ्यास
4 Videos
- अणुगति सिद्धांतBOOK - SCIENCE PUBLICATIONCHAPTER - अणुगति सिद्धांतEXERCISE - अन्य महत्तवपूर्ण प्रश्न
7 Videos
- अणुगति सिद्धांतBOOK - SCIENCE PUBLICATIONCHAPTER - अणुगति सिद्धांतEXERCISE - बोधात्मक प्रश्न
15 Videos
- उष्मागतिकीBOOK - SCIENCE PUBLICATIONCHAPTER - उष्मागतिकीEXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
28 Videos
Similar Questions
1 मीटर लंबी संकरी (और एक सिरे पर बंद) नली क्षैतिज रखी गई है। इसमें 76 cm लंबाई भरा पारद सूत्र, वायु के 15 cm स्तम्भ को नली में रोककर रखता है। क्या होगा यदि खुला सिरा नीचे की ओर रखते हुए नली को ऊर्ध्वाधर कर दिया जाए?
View Solutionअणुगति सिद्धांत के आधार पर ताप की व्याख्या करो।
View Solutionवास्तविक गैस, समीकरण PV=RT का कब अधिक सही पालन करती है?
View Solutionएक निकाय का P-V आरेख जो कि ऊष्मागतिकी परिवर्तन प्रदर्शित करता है। चित्र में दर्शाया गया है। निकाय पर किया गया कार्य A→B→C 50J है ,आंतरिक ऊर्जा में परिवर्तन ज्ञात कीजिये,दी गई ऊष्मा 84 J है।
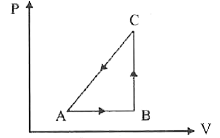
View Solutionएक द्विआधारी संख्या (cdccddcccddd)2 से निरूपित की जाती है, जहाँ c>d है । इसका दशमलव तुल्य क्या है ?
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View Solutionयदि किसी घन का आयतन 125cm3 है, तो उसकी भुजा की लम्बाई क्या होगी?
View Solutionएक मशीन का मूल्य 7500 रुo है। इसका मूल्य 5% वार्षिक दर से घट रहा है तब एक वर्ष बाद इसका मूल्य क्या होगा?
View SolutionIf the total surface area of a cube is 1944m2, then find the volume of the cube :
यदि एक घन का पृष्ठ क्षेत्रफल 1944m2 है , तो इसका आयतन है :
View Solution27^@C पर एक अभिक्रिया के लिए K_p से K_c का अनुपात 24.63 L atm mol^(-1) है। यदि नियत दाब पर अभिक्रिया की ऊष्मा 98.8 kcal है, तो नियत आयतन पर अभिक्रिया की ऊष्मा (kcal में) क्या होगी?
View Solutionआयोडीन एक ठोस है और साधारण ताप पर ऊर्ध्वपातित होता है। इसका कारण है:
View SolutionNTP पर O_2 का घनत्व 16 है। किस ताप पर ( ""^@C में) इसका घनत्व 14 होगा? यह मानते हुए कि दाब नियत रहता है।
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@) = 0.4 और P_(B)^(@) = 1.2 atm है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View Solution50^(@)C और 3 atm के दाब पर एक 2 L का पात्र वायु से भरा हुआ है। अब ताप को 200^(@)C तक बढ़ा दिया जाता है। एक वाल्व को खोला जाता है ताकि उसके अंदर का दाब 1 atm हो जाए। वाल्व को खोलने पर मुक्त होने वाले मोलों की संख्या का मोल प्रभाज क्या होगा? (माना लीजिए कि पात्र के आयतन में कोई परिवर्तन नहीं होता है)
View Solution400 K ताप पर, 20 लीटर के एक पात्र में 0.4 atm दाब पर CO2(g) और SrO का आधिक्य (ठोस SrO के आयतन की उपेक्षा कीजिए) उपस्थित होता है | अब पात्र में लगे गतिशील पिस्टन को गतिमान करके पात्र का आयतन कम कर दिया जाता है | जब CO2 का दाब अपना अधिकतम मान प्राप्त करता है तो पात्र का अधिकतम आयतन क्या होगा ? (दिया गया है कि: SrCO3(S)⇔SrO(s)+CO2(g),Kp=1.6atm)
View Solution15∘C ताप और 1.5 bar दाब पर वायु का एक बुलबुला अंतर्जलीय होता है। यदि बुलबुला सतह पर आ जाता है जहाँ 25∘C ताप और 1.0 bar दाब होता है तो बुलबुले के आयतन का क्या होगा?
View Solution
