The angle of prism is 60∘ and its refractive index is 1.5. There will be no emergent light if the angle of incidence on the first face is
equal to 30∘
less than 27∘
more than 30∘
equal to 60∘
The correct Answer is:B
To determine the angle of incidence on the first face of a prism with an angle of 60 degrees and a refractive index of 1.5, such that there will be no emergent light, we can follow these steps:
1. Understanding the Condition for No Emergent Light:
- For no emergent light to occur, the light must undergo total internal reflection (TIR) at the second face of the prism. This happens when the angle of refraction at the second face is 90 degrees (grazing condition).
2. Identify Angles:
- Let the angle of incidence on the first face be i.
- The angle of the prism is given as A=60∘.
- Let R1 be the angle of refraction at the first face and R2 be the angle of refraction at the second face.
3. Using the Prism Formula:
- The relationship between the angles in the prism is given by:
R1+R2=A
- Since we want R2=90∘ for TIR, we can substitute:
R1+90∘=60∘
- This gives us:
R1=60∘−90∘=−30∘
- This indicates that for R2 to be 90 degrees, R1 must be 60∘.
4. Applying Snell's Law:
- At the first face, Snell's law states:
n1sin(i)=n2sin(R1)
- Here, n1=1 (air), n2=1.5 (glass), and R1=60∘.
- Thus, we have:
sin(i)=1.5sin(60∘)
5. Calculating sin(60∘):
- We know that sin(60∘)=√32.
- Therefore:
sin(i)=1.5⋅√32=1.5√32
6. Finding the Angle of Incidence i:
- To find i, we take the inverse sine:
i=sin−1(1.5√32)
- This value will give us the angle of incidence at which TIR occurs.
7. Conclusion:
- The angle of incidence i must be less than the calculated value for there to be no emergent light.
Final Answer:
The angle of incidence on the first face must be less than approximately 27∘ for there to be no emergent light.
- For no emergent light to occur, the light must undergo total internal reflection (TIR) at the second face of the prism. This happens when the angle of refraction at the second face is 90 degrees (grazing condition).
- Let the angle of incidence on the first face be i.
- The angle of the prism is given as A=60∘.
- Let R1 be the angle of refraction at the first face and R2 be the angle of refraction at the second face.
- The relationship between the angles in the prism is given by:
R1+R2=A
- Since we want R2=90∘ for TIR, we can substitute:
R1+90∘=60∘
- This gives us:
R1=60∘−90∘=−30∘
- This indicates that for R2 to be 90 degrees, R1 must be 60∘.
- At the first face, Snell's law states:
n1sin(i)=n2sin(R1)
- Here, n1=1 (air), n2=1.5 (glass), and R1=60∘.
- Thus, we have:
sin(i)=1.5sin(60∘)
- We know that sin(60∘)=√32.
- Therefore:
sin(i)=1.5⋅√32=1.5√32
- To find i, we take the inverse sine:
i=sin−1(1.5√32)
- This value will give us the angle of incidence at which TIR occurs.
- The angle of incidence i must be less than the calculated value for there to be no emergent light.
The angle of incidence on the first face must be less than approximately 27∘ for there to be no emergent light.
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(More than one correct choice type)
14 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Linked Comprehension)
2 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems
44 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
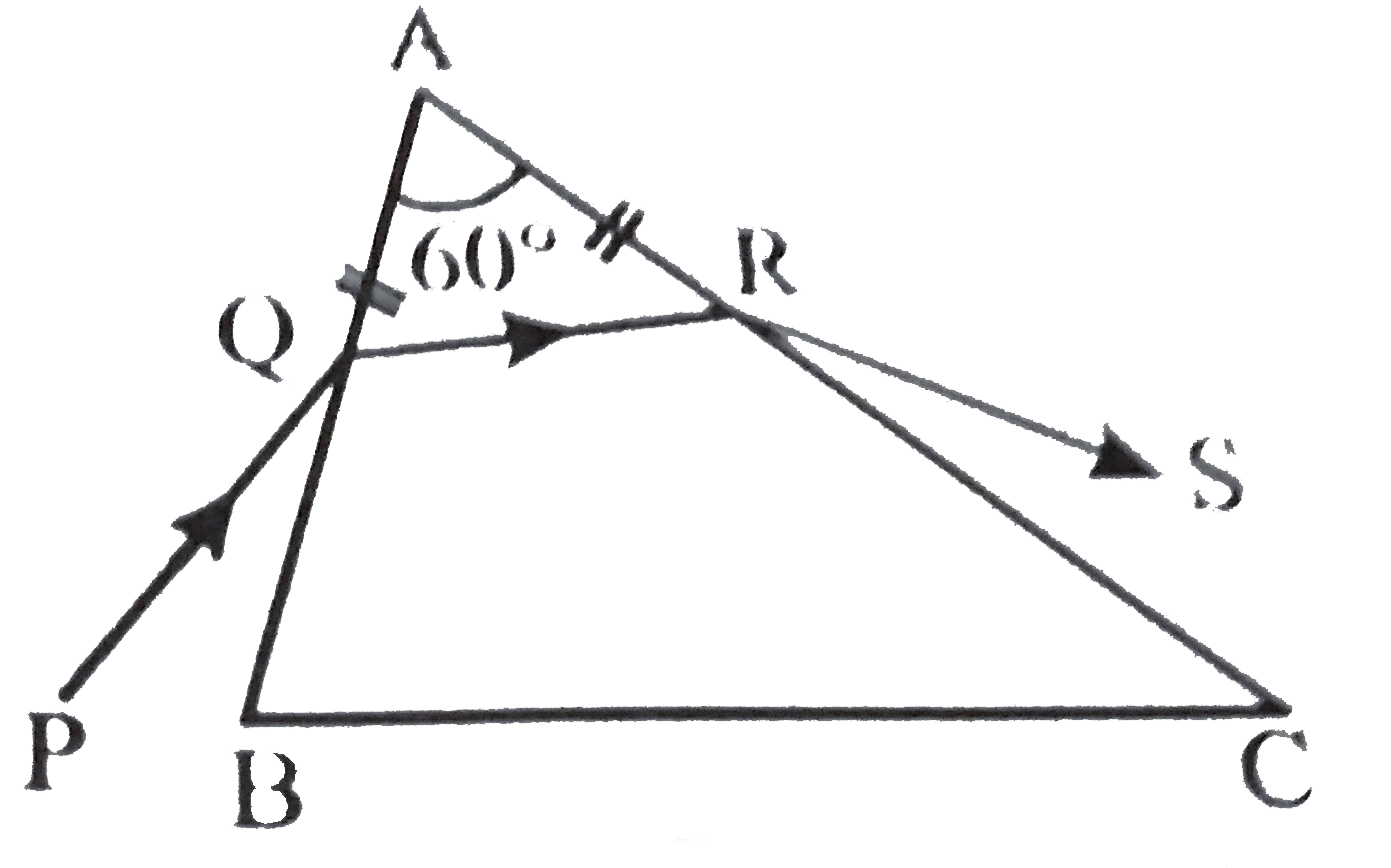
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the meterial of prism is √2 , then the angle of deviation of the ray is
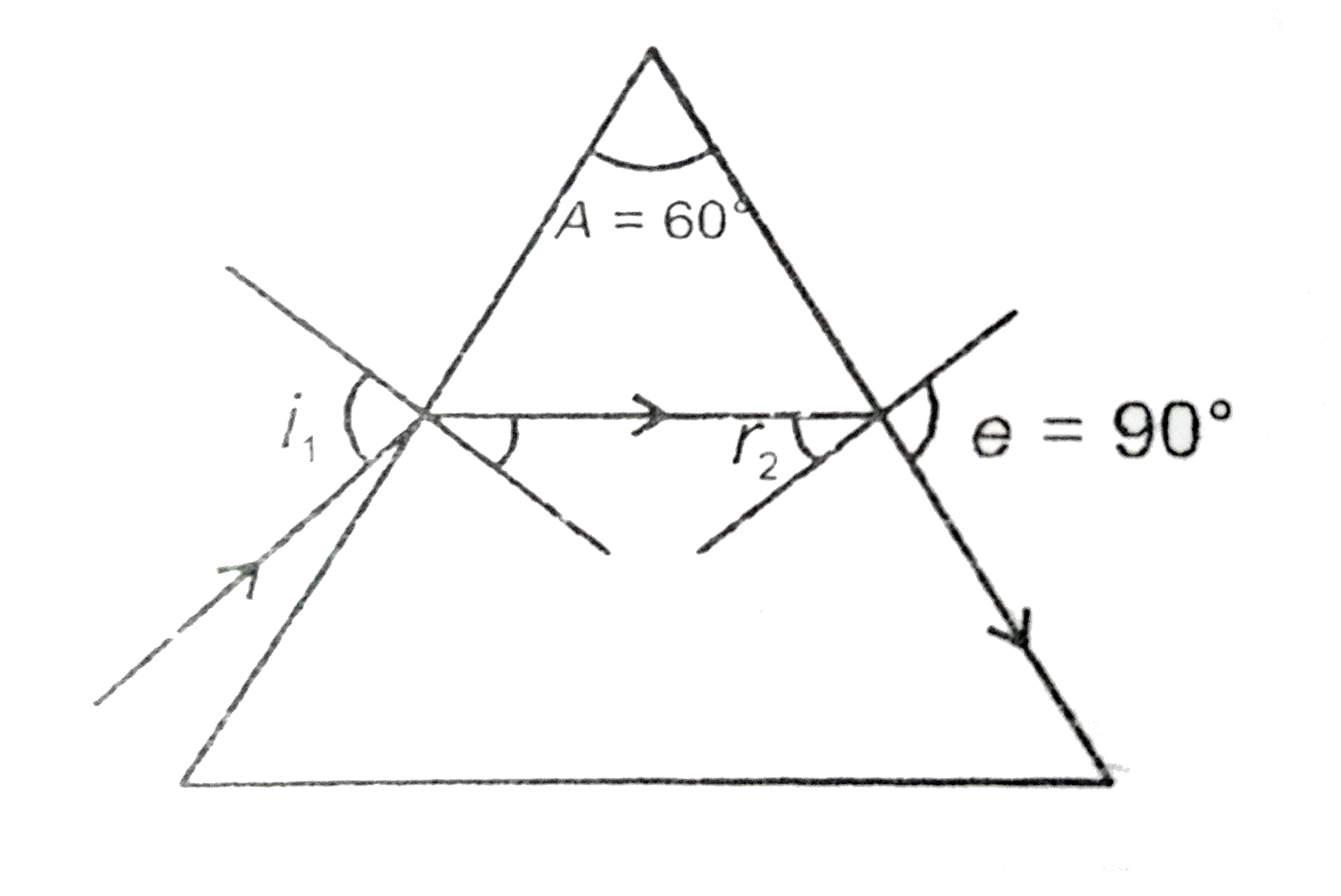
View SolutionCalculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.
View Solution
Knowledge Check
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the material of prism is 3, then the angle of deviation of the ray is
 A60∘B45∘C30∘DNone of the above
A60∘B45∘C30∘DNone of the aboveA ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2 , the angle of incidence on the first face of the prism is
A30∘B45∘C60∘D0∘A ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2, the angle of incidence on the first face of the prism is
A30∘B45∘C60∘D0∘
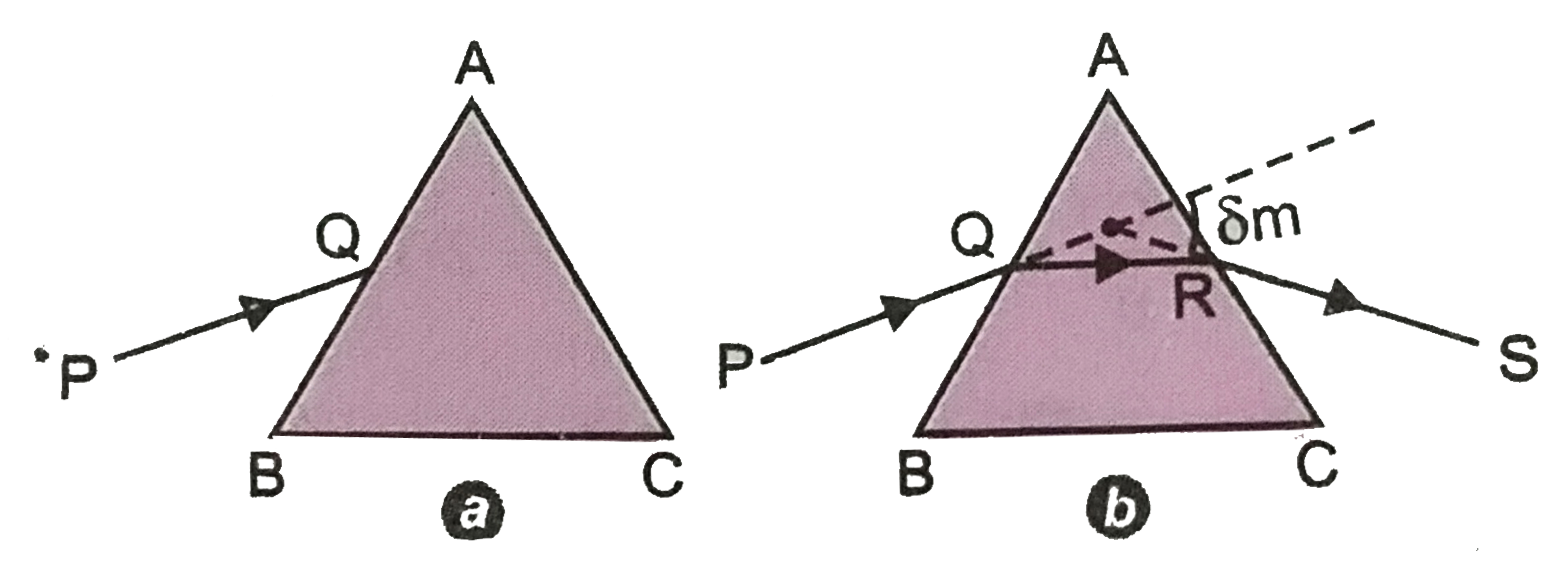
A ray PQ incident on face AB of a prism ABC, as shown in Fig., emerges from the face AC such that AQ=AR. Draw the ray diagram showing the pasage of the ray through the prism. If the angle of prism is 60∘ and refractive index of the material of the prism is √3, determine the values of angle of incidence and angle of deviation.
 .
.
View SolutionThe refracting angle of a glass prism is 60∘ and μ of its material is 1.45. Calculate angle of incidence at the first that will just reflect internaly the ray at the second face.
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes thorugh the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2, the angle of incidence on the first face of the prism is
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of refracting angle75∘ . It passes through the prism and is incident on the other face at the critical angle If the refracive index of the material of prism is √2, the angle of incidence on the first face o the prism is
View SolutionA ray of monochromatic light is incident on the refracting face of a prism (angle 75∘0 . It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the prism is √2 , then the angle of incidence on the first of the prism is
View Solution
