A sound source emits two sinusoidal sound waves, both of wavelength λ, along paths A and B as shown in figure.The sound travelling along path B is reflected from five surfaces as shown and then merges at point Q, producing minimum intensity at that point.The minimum value of d in terms of λ is :

Because the two waves emerge from the same source, they must emerge in phase with each other. When they merge at point their phase difference can depend only on the path length difference ΔL between the two paths they followed.
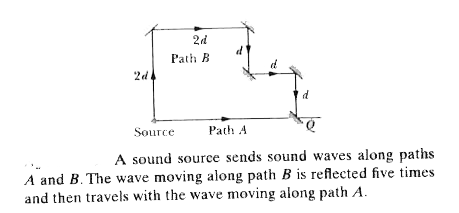
To reach Q , the wave following path A travels distance 3d, and the wave following path B travels distance 7d. thus , their path length difference ΔL is 4d.
If the waves are to be exactly out of phase at Q, we must have
ΔLλ=0.5,1.5,2.5,...
Substituting ΔL=4d and solving for d then give us
d=18λ,38λ,58λ,..............
Similarly , if the waves are to be exactly in phase at point Q, we must have
ΔLλ=0,1,2,3........
We can eliminate 0 from the list (which that there is no path difference in fig. ) . solving for d, we find
d=14λ,12λ,34λ .........
Topper's Solved these Questions
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - CHECKPOINTS
4 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PROBLEMS
59 Videos
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS
39 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
The number of ways in which a person can reach from the point A to B along the grid through the shortest path as shown in the figure is -
View SolutionIn Fig., sound waves A and B, both of wavelength λ , are initially in phase and traveling rightward, as indicated by the two rays. Wave A is reflected from four surfaces but ends up traveling in its original direction. Wave B ends in that direction after reflecting from two surfaces. Let distance L in the figure be expressed as a multiple q of λ:L=qλ. What are the (a) smallest and (b) third smallest values of q that put A and B exactly out of phase with each other after the reflections?
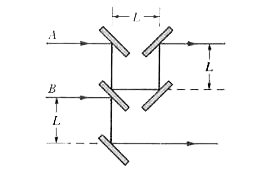
View Solution
Knowledge Check
A sound wave of wavelength 32 cm enters the tube at S as shown in the figure. Then the smallest radius r so that a minimum of sound is heard at detector D is
 A7cmB14cmC21cmD28cm
A7cmB14cmC21cmD28cmIn the figure shown, light waves A and B both of wavelength λ are initially in phase and travelling rightward as incident by the two rays. Wave A is reflected from four parallel surfaces but ends up travelling in original direction. The possible value(s) of distance L in terms of wavelength λ in figure which put A and B exactly out of phase with each other after all the reflected is/are
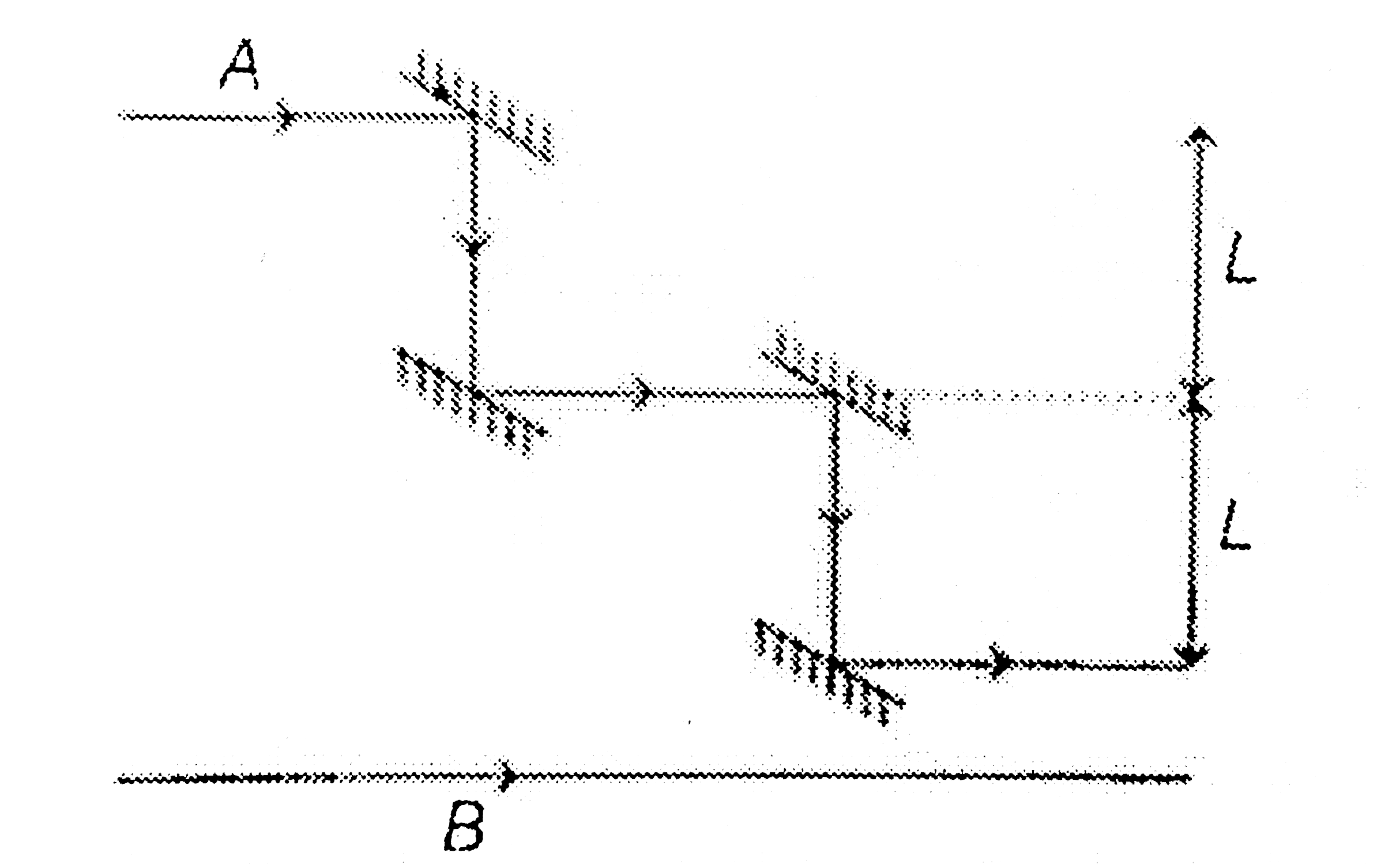 Aλ/2B3λ/2C3λ/4Dλ
Aλ/2B3λ/2C3λ/4DλTwo sound sources emitting sound each of wavelength λ are fixed at a given distance apart. A listener moves with a velocity u along the line joining the two suorces. The number of beats heard by him per second is
A2uλBuλCu3λD2λu
Two sound sources emitting sound each of wavelength λ are fixed at a given distance apart. A listener moves with a velocity u along the line joining the two suorces. The number of beats heard by him per second is
View SolutionA sound wave having wavelength λ froms stationary waves after reflection from a surface . The distace between two consecutive nodes is
View Solution2 loudspeakers are emitting sound waves of wavelength lambda with an initial phase difference of π2 at what minimum distance from O on line AB will one hear a maximum

View SolutionTwo coherent sound sources A and B produce a sound of wavelength λ. If at t=0 a detector starts moving with constant velocity v0 from point O along y - direction, then the minimum time, after which it detects the sound of maximum intensity, is (D>>λ)
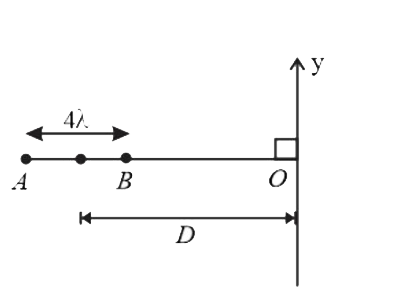
View SolutionTwo separated sources emit sinusoidal travelling waves but have the same wavelength λ and are in phase at their respective sources . One travels a distance l1 to get to the observeration point while the other travels a distance l2 . The amplitude is minimum at the observation point , l1−l2 is an
View Solution
