A car of mass $m$ travelling at speed $v$ moves on a horizontal track. The centre of mass of the car describes a circle of radius $r$ . If $2 a$ is the separation of the inner and outer wheels and $h$ is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
$v^{2} = \frac{g r a}{h}$

Video Solution

Text Solution

Verified by Experts

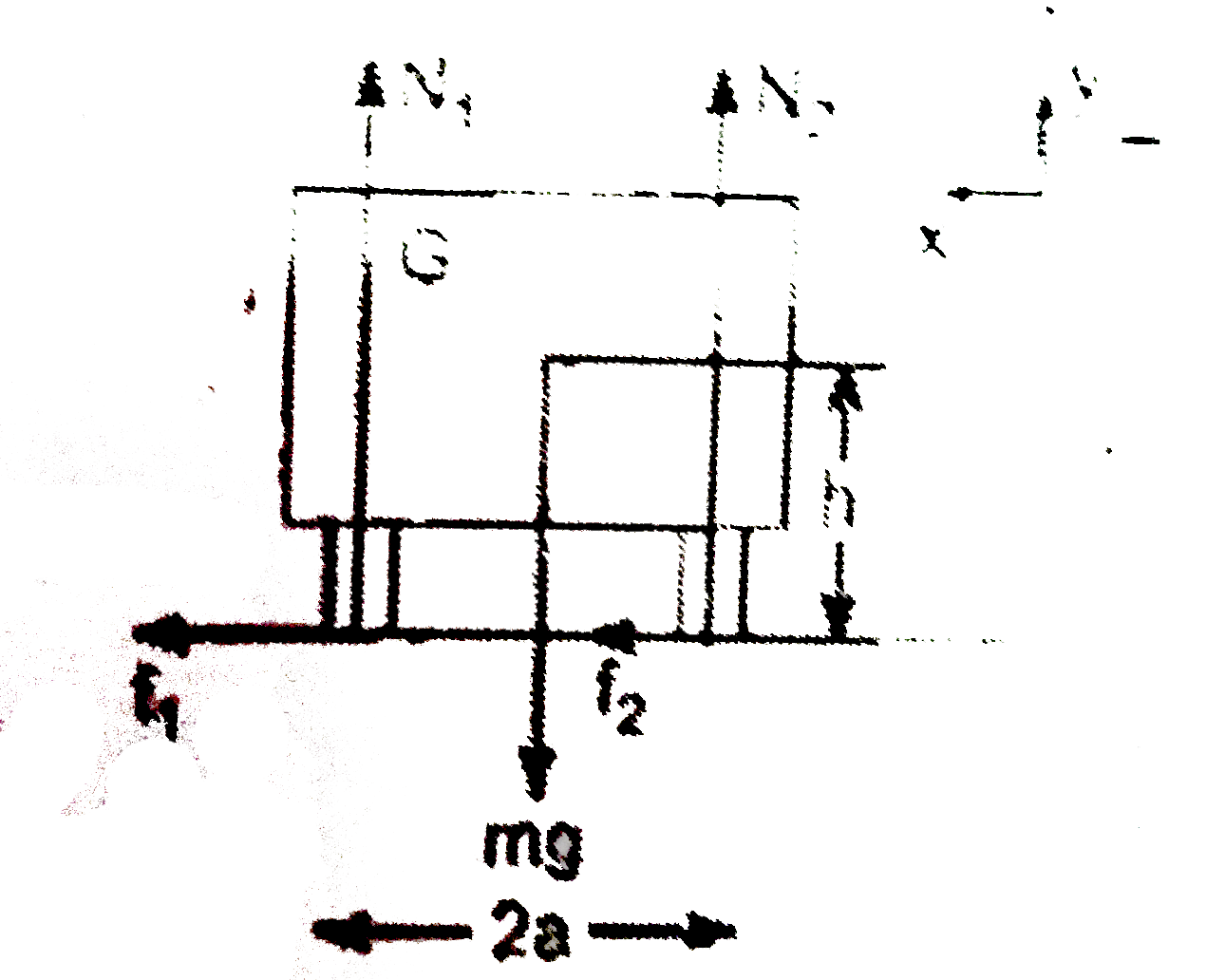
Figure 11-22a shows the rear view of the car that is turn ing toward left. If you have watched any action movie where car overturns, you may know that it overturns outward of the curve when traveling at a high speed.
Frictional force on the tires provides a centripetal force while turning. When car is going at a high speed, the inner tires will lose contact with the ground. We can consider car in equilibrium in its own frame .

Calculations: As it will be a non-inertial reference frame, we need to apply pseudo centrifugal force
$\sum F_{x} = F_{1} + f_{2} - \frac{m v^{2}}{r} = 0$ (11-32)
$\sum F_{x} = F_{N_{1}} + f_{N_{2}} - m g = 0$ (11-33)
From condition of rotational equilibrium, sum of moments about center of mass G must be zero:
$\sum τ = (f_{1} + f_{2}) h + F_{N_{1}} a - F_{N_{2}} a = 0$ (11-34)
$f_{1} + f_{2} = (F_{N_{1}} - F_{N_{2}}) \frac{a}{h}$ (11-35)
On combining Eqs. 11-32 and 11-35, we can eliminate $f_{1} + f_{2}$ to obtain
$F_{N_{1}} - F_{N_{2}} = \frac{m v^{2} h}{a r}$ (11-36)
Now, we can solve Eqs. 11-33 and 11-36 simultaneously to obtain
$2 F_{N_{1}} = m g - \frac{m v^{2} h}{r}$ and $2 F_{N_{2}} = m g + \frac{m v^{2} h}{r}$
The inner wheels will leave the ground when $N_{1}$ becomes zero, that is,
$m g = \frac{m v^{2} h}{a r}$
$v^{2} = \frac{g r a}{h}$
Learn: As expected in Eq. 11-36, we can see that as v increases the $F_{N_{1}}$ , will decrease and car will overturn out wardly.
If frictional force is not sufficient to provide centripetal acceleration, sideways skidding will occur instead of overturning.
$f_{1} + f_{2} \leq μ (F_{N_{1}} - F_{N_{2}})$
Equality sign holds when skidding starts:
$F_{N_{1}} - F_{N_{2}} = m g$
and $f_{1} + f_{2} = \frac{m v^{2}}{r}$
Therefore, the limiting speed at which skidding occurs is given by $v^{2} + μ g r$ . If the car is to skid rather than overturn,
$μ g r < \frac{g r a}{h}$ or $μ < \frac{a}{h}$

Updated on:21/07/2023

A car while travelling at a speed of 72 km/hr. Passes through a curved portion of road in the form of an arc of a radius 10 m. If the mass of the car is 500 kg the reaction on the car at the lowest point P is-
A25 KN
B50 KN
C75 KN
DNone of these
A car moves with speed $v$ on a horizontal circular track of radius $R$ . A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is $h$ , and the separation between its inner and outer wheels is $d$ The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
.
A $\sqrt{\frac{g R d}{2 h}}$
B $\sqrt{\frac{g R d}{h}}$
C $\sqrt{\frac{2 g R d}{h}}$
D $\sqrt{\frac{2 g R d}{3 h}}$
A car of mass $m$ moves in a horizontal circular path of radius $r$ metre. At an instant its speed is $V m / s$ and is increasing at a rate of $a m / {sec}^{2}$ .then the acceleration of the car is
A $\frac{V^{2}}{r}$
B $a$
C $\sqrt{a^{2} + {(\frac{V^{2}}{r})}^{2}}$
D $\sqrt{a + (\frac{V^{2}}{r})}$