A wire of length l, mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle θ with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
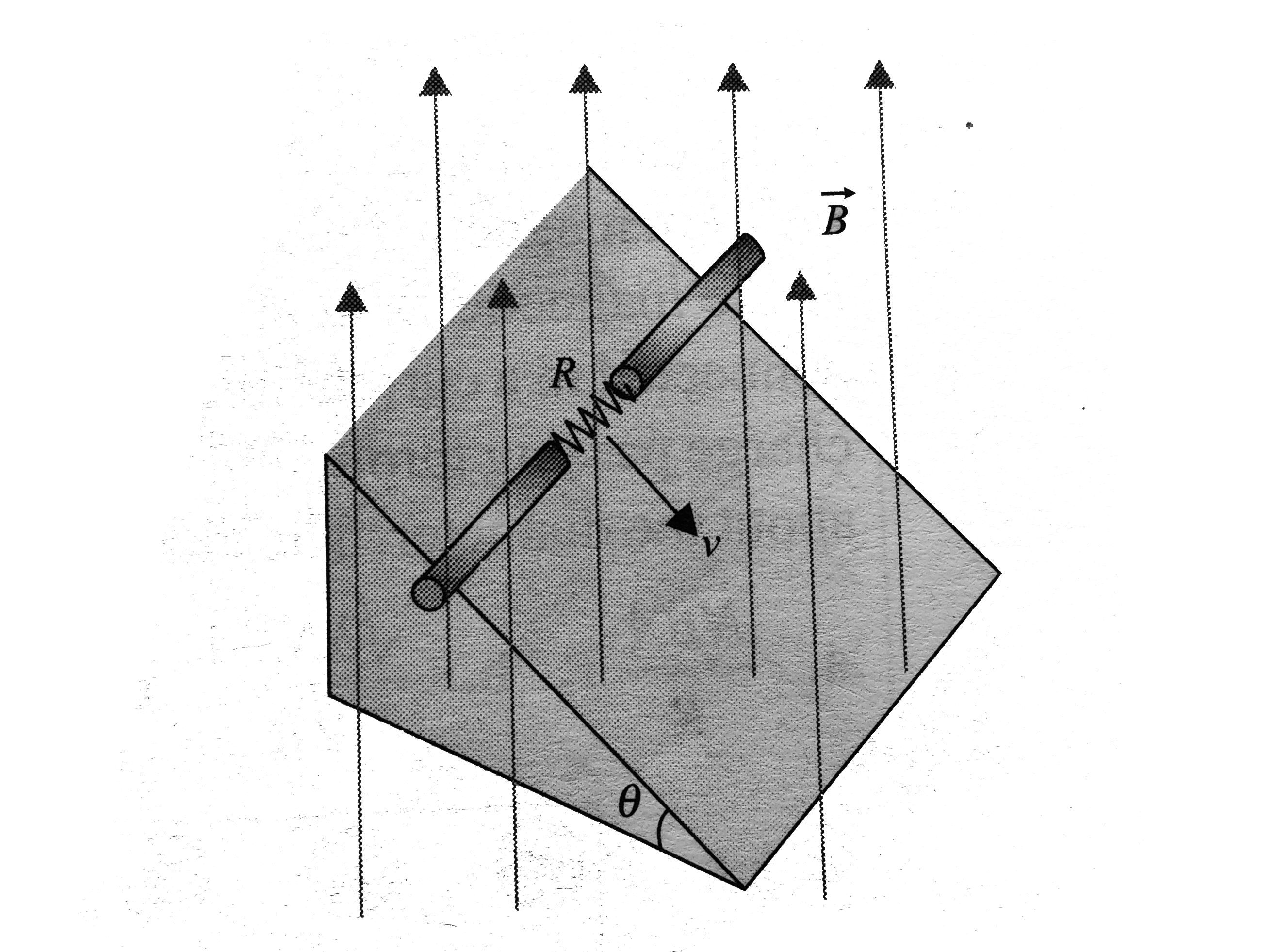
(a) First method: Let us assume that the rod has acquired a velocity v. By applying the concept of motional emf (Eq. 30-9), the emf of the rod is
ΔV=(→v×→B).l=Blvcosθ
This emf will be such that the current is flowing toward the observer as in Fig. 30-21. The resulting current at that instant is
i=ΔVR=BlvcosθR
Applying Eq. 28-29, we get
∣∣→F∣∣=∣∣i→l×→B∣∣=B2l2vcosθR
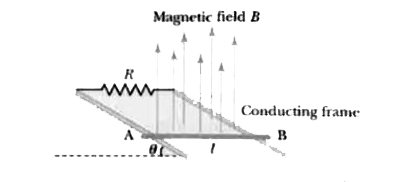
figure 30-20 A conducting rod is released from rest on a smooth conducting frame inclined at an angle θ to the horizontal.
This force is directed horizontally. A component of this force will oppose the motion of the rod as can be seen in Fig. 30-21.
Hence the acceleration of the rod is given by
mgsinθ−B2l2vcos2θR=ma
It can be easily seen that the acceleration of the rod decreases as its velocity increases. After a long time, the acceleration of the rod will tend to zero. The velocity of the rod at this instant is known as the terminal velocity:
vT=mgRsinθB2l2cos2θ
(b) Second method:
Let us find the rate of work done by gravity when the velocity of the rod is v.
We know that the power developed by gravity is
p=→F.→v=mgvsinθ
The rate at which power will be dissipated is
Pd=(ΔV)2R=(Blvcosθ)2R

Figure 30-21 A figure showing the direction of current flow and the force on the rod.
In steady state,
mgvsinθ=(Blvcosθ)2R
vT=mgRsinθB2l2cos2θ
which is the same as before.
We can also find the velocity of the rod as a function of time. Put
a=dvdt
We get
dvdt=gsinθ(1−vvt)
By integrating, we get
v=vT(1−e−gsinθt/vr)
The equation can be easily checked. By substituting t = 0, the velocity turns out to be zero, as expected. At t=∞, the velocity turns out to be vT.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PROBLEMS
67 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
The graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, with the direction of the field perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first.

View SolutionIn Fig. 30-37, a metal rod is forced to move with constant velocity →v along two parallel metal rails, connected with a strip of metal at one end. A magnetic field of magnitude B = 0.125 T points out of the page. ( a) If the rails are separated by L = 25.0 cm and the speed of the rod is 38.0 emfs, what emf is generated? (b) If the rod has a resistance of 18.0 Ω and the rails and connector have negligible resistance, what is the current in the rod? (c) At what rate is energy being transferred to thermal energy? (d) What is the magnitude of the leftward force that causes the rod to move?
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
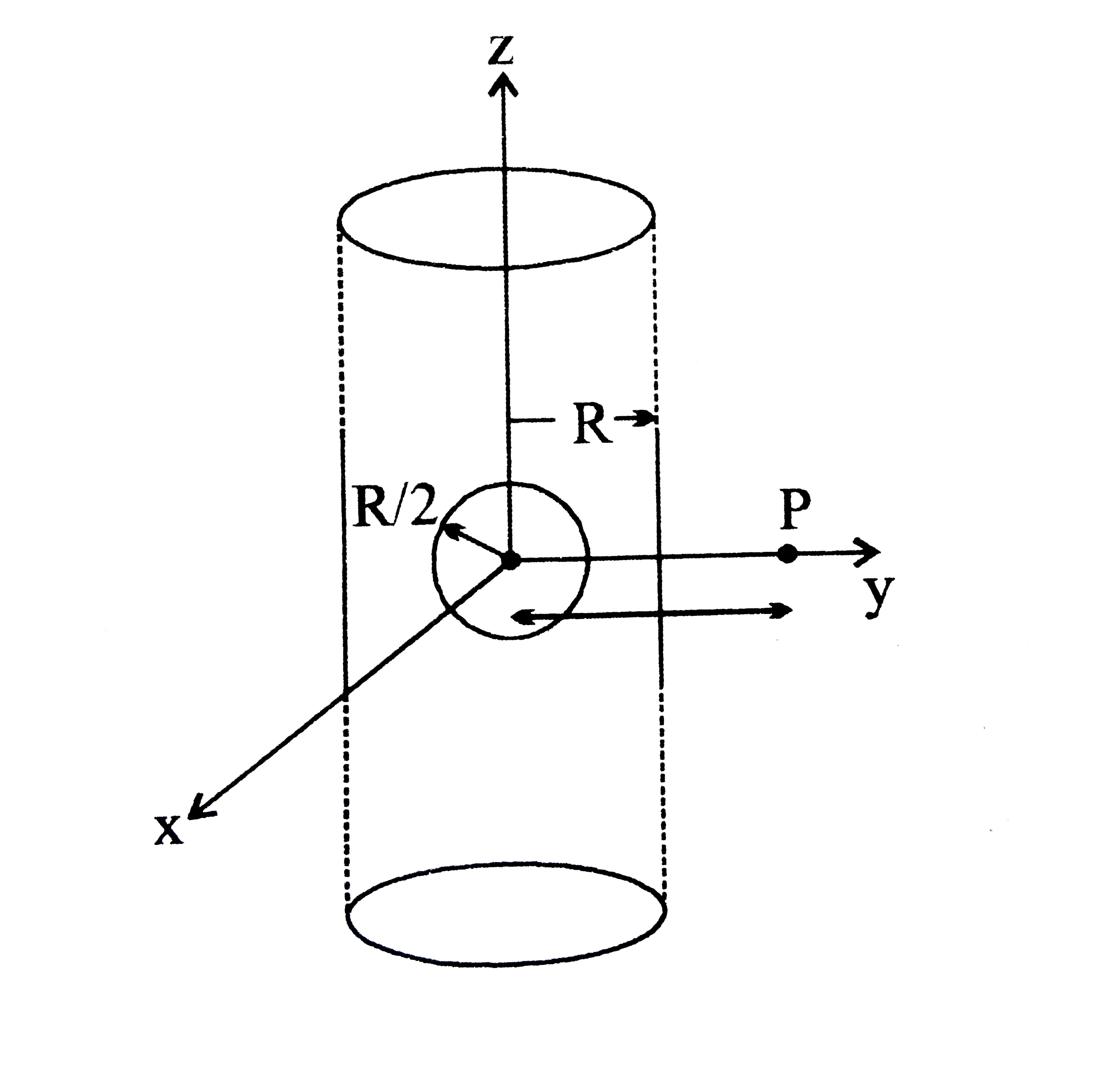 .
.
View SolutionAn a.c source of frequency 1000Hz is connected to a coil of 200πmH and negligible resistance. If effective current through the coil is 7.5mA, what is the voltage (in volt) across the coil ?
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA wire of length l , mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View SolutionConsider parallel conducting rails separated by a distance l. There exists a uniform magnetic field B perpendicular to the plane of the rails as shown in Fig. Two conducting wires each of length l are placed so as to slide on parallel conducting rails. One of the wires is given a velocity v0 parallel to the rails. Till steady state is achieved, loss in kinetic energy of the system is
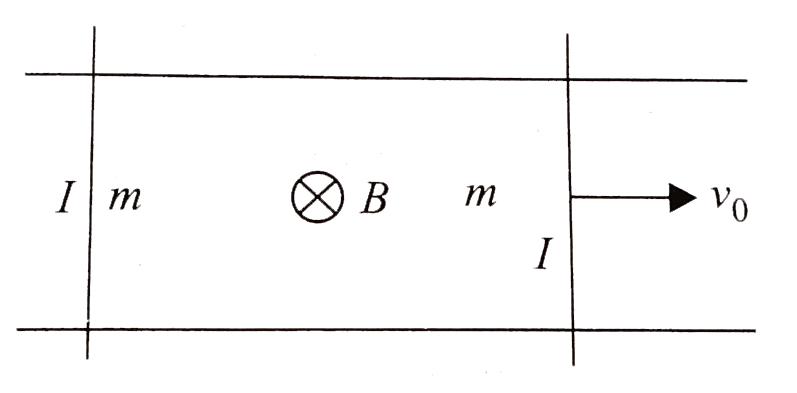
View SolutionA wire cd of length l and mass m is sliding without friction on conducting rails ax and by as shown. The verticle rails are connected to each other with a resistance R between a and b . A uniform magnetic field B is applied perpendicular to the plane abcd such that cd moves with a constant velocity of
View SolutionA pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Omega and 5Omega are to slide without friction along the rail. The distance between the conducting rails is 0.1m . Then
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle theta to the horizontal. At the bottom, the rails are joined by a resistance R . There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
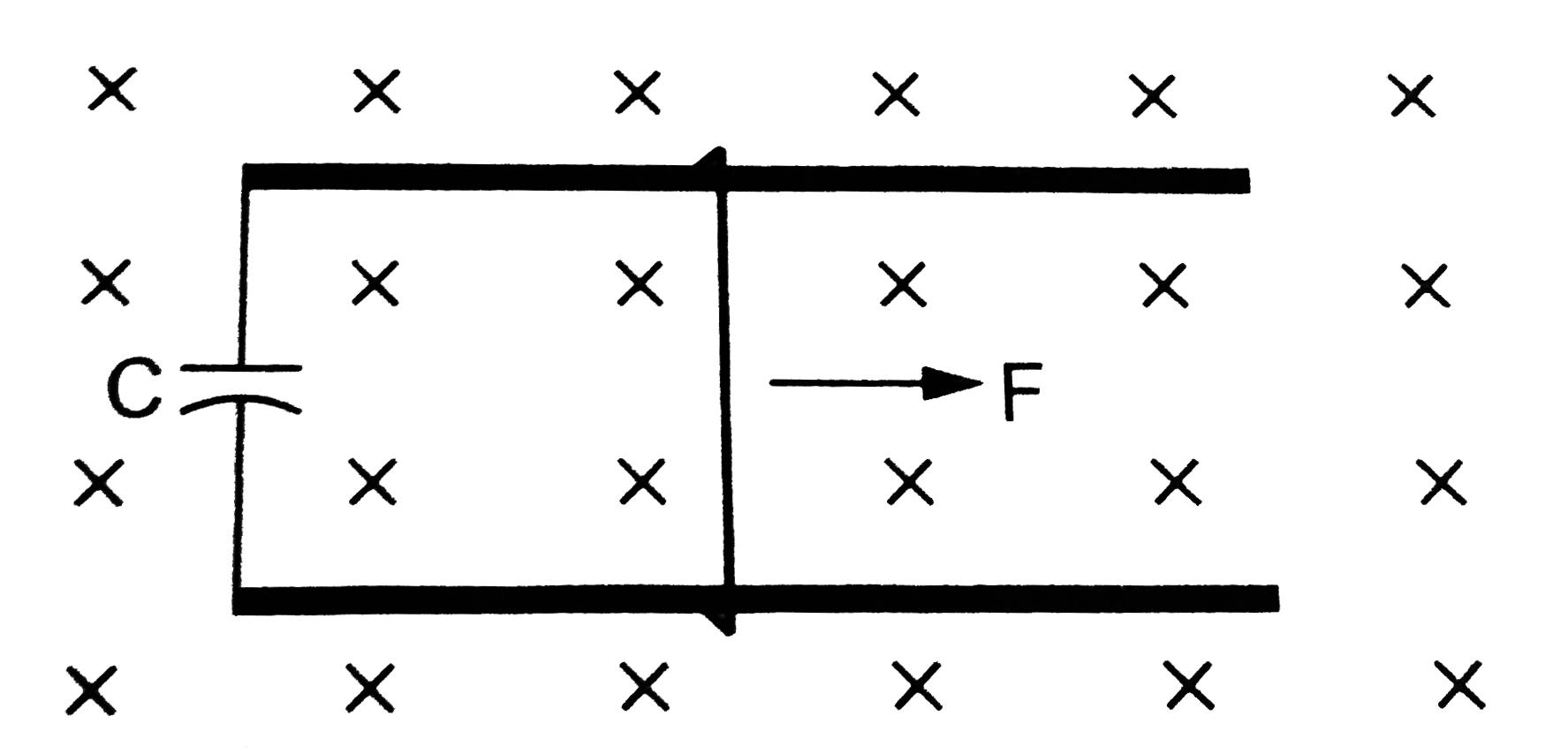
View SolutionA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle theta with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View Solutionएक कॉपर की छड़ का द्रव्यमान m है। यह दो क्षैतिज समान्तर चिकनी पटरियों (rails) जिनके बीच की दूरी । है तथा क्षैतिज के साथ θ कोण बनाती है, पर गुरुत्व के अन्तर्गत फिसलती है। तली में पटरियाँ एक प्रतिरोध R के द्वारा चित्रानुसार जुड़ी हैं। यहाँ एकसमान चुम्बकीय क्षेत्र B पटरियों (rails) के तल के लम्बवत् है। छड़ का क्रान्तिक वेग है

View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
View SolutionConsider parallel conducting rails separated by a distance l. There exists a uniform magnetic field B perpendicular to the plane of the rails as shown in Fig. Two conducting wires each of length l are placed so as to slide on parallel conducting rails. One of the wires is given a velocity v_(0) parallel to the rails. Till steady state is achieved, loss in kinetic energy of the system is
View Solution
