Two circles intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is
PT = 2PQ
PT<PQ
PT>PQ
PT=PQ
The correct Answer is:D
Step by step video, text & image solution for Two circles intersect at A and B. P is a point on produced BA. PT and PQ are tangents to the circles. The relation of PT and PQ is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
As per the figure, two circles intersect each other at points P and Q. Point A is on PQ produced and AMD and ASR are the secants to the circles. If AM = 3, MD = 5, AS = 4, The value of SR is :
View SolutionTwo circles with centers O and O' of radii 6cm and 8 cm respectively intersect two points P and Q such that OP and O'P are tangents to the two circle. The length of the common chord PQ is
View Solution
Knowledge Check
Two circles touch each other externally at point A and PQ is a direct tangent which touch circle at P and Q respectively then ∠PAQ = ?
A45∘B90∘C80∘D100∘
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm , respectively intersect at two points P and Q such that OP and O'P are tangents to the two circle . Find the length of the common chord PQ.
View SolutionTwo circles intersect at two points P and S. QR is a tangent to the two circles at Q and R. If ∠QSR=72∘, then ∠QPR=.
View SolutionIn figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.

View SolutionPQ and RS are common tangents of two circles intersection at A and B. AB, when produced both sides, meet the tangents PQ and RS at x and y, respectively. If AB = 3 cm, xy = 5 cm, then PQ (in cm) will be.
View SolutionDraw the tangent, if two circle intersecting in two points.
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
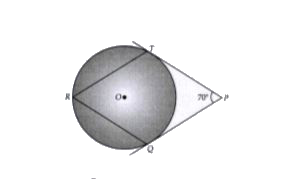
View Solution
