A particle starting from rest falls from a certain height. Assuming that the acceleration due to gravity remain the same throughout the motion, its displacements in three successive half second intervals are S1,S2andS3 then
S1:S2:S3=1:5:9
S1:S2:S3=1:3:5
S1:S2:S3=9:2:3
S1:S2:S3=1:1:1
The correct Answer is:B
To solve the problem of a particle falling from rest under the influence of gravity, we need to find the displacements S1, S2, and S3 during three successive half-second intervals. Let's break this down step by step.
Step 1: Understand the Motion
The particle starts from rest, meaning its initial velocity u=0. The acceleration due to gravity g is constant throughout the motion. We will use the second equation of motion:
S=ut+12gt2
Step 2: Calculate S1
For the first half-second interval (from t=0 to t=0.5 seconds):
- Initial velocity u=0
- Time t=0.5 seconds
Using the equation:
S1=0⋅(0.5)+12g(0.5)2=12g⋅14=g8
Step 3: Calculate S2
For the second half-second interval (from t=0.5 to t=1.0 seconds):
- The total time is now t=1.0 seconds.
- The displacement from the start to t=1.0 seconds is:
Stotal=12g(1.0)2=g2
- The displacement S2 is the total displacement at t=1.0 seconds minus the displacement at t=0.5 seconds:
S2=Stotal−S1=g2−g8=4g8−g8=3g8
Step 4: Calculate S3
For the third half-second interval (from t=1.0 to t=1.5 seconds):
- The total time is t=1.5 seconds.
- The displacement from the start to t=1.5 seconds is:
Stotal=12g(1.5)2=12g⋅94=9g8
- The displacement S3 is the total displacement at t=1.5 seconds minus the displacement at t=1.0 seconds:
S3=Stotal−(S1+S2)=9g8−(g8+3g8)=9g8−4g8=5g8
Step 5: Find the Relationship Between S1,S2,S3
Now we have:
- S1=g8
- S2=3g8
- S3=5g8
To find the ratio S1:S2:S3:
S1:S2:S3=g8:3g8:5g8=1:3:5
Final Answer
The relationship between the displacements is:
S1:S2:S3=1:3:5
The particle starts from rest, meaning its initial velocity u=0. The acceleration due to gravity g is constant throughout the motion. We will use the second equation of motion:
S=ut+12gt2
For the first half-second interval (from t=0 to t=0.5 seconds):
- Initial velocity u=0
- Time t=0.5 seconds
S1=0⋅(0.5)+12g(0.5)2=12g⋅14=g8
For the second half-second interval (from t=0.5 to t=1.0 seconds):
- The total time is now t=1.0 seconds.
- The displacement from the start to t=1.0 seconds is:
Stotal=12g(1.0)2=g2
- The displacement S2 is the total displacement at t=1.0 seconds minus the displacement at t=0.5 seconds:
S2=Stotal−S1=g2−g8=4g8−g8=3g8
For the third half-second interval (from t=1.0 to t=1.5 seconds):
- The total time is t=1.5 seconds.
- The displacement from the start to t=1.5 seconds is:
Stotal=12g(1.5)2=12g⋅94=9g8
- The displacement S3 is the total displacement at t=1.5 seconds minus the displacement at t=1.0 seconds:
S3=Stotal−(S1+S2)=9g8−(g8+3g8)=9g8−4g8=5g8
Now we have:
- S1=g8
- S2=3g8
- S3=5g8
S1:S2:S3=g8:3g8:5g8=1:3:5
The relationship between the displacements is:
S1:S2:S3=1:3:5
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-170videos
MOTION IN A STRAIGHT LINE
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR28videos
MOTION IN A PLANE
- BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 2 : Concept Applicator25videos
MOVING CHARGES AND MAGNETISM
Similar Questions
A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of time in successive displacement d.
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
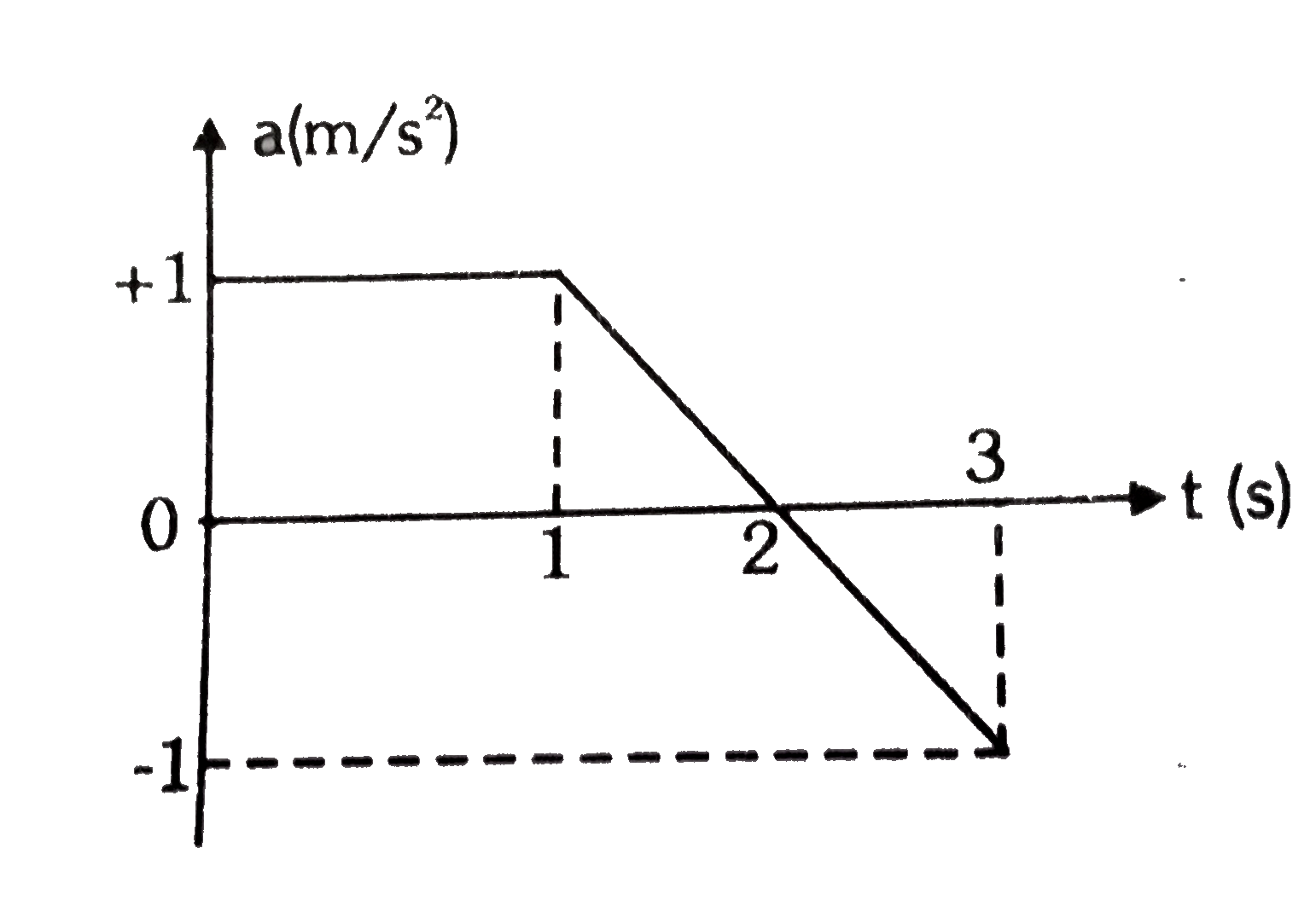View Solution
Knowledge Check
- Question 1 - Select One
A particle starting from rest attains a velocity of 50ms−1 in 5 s. The acceleration of the particle is
A5ms2B10ms2C50ms2D100ms2 - Question 2 - Select One
A particle is dropped from rest from a large height Assume g to be constant throughout the motion. The time taken by it to fall through successive distance of 1m each will be :
Aall equal, being equal to √2/g secondBin the ratio of the square roots of the integers 1,2,3,…..Cin the ratio of the difference in the square roots of the integers, i.e.,
√1,(√2−√1),(√3−√2),(√4−√3), ….Din the ratio of the reciprocals of the square roots of the integers, i.e., 1√1,1√2,1√3,….. - Question 3 - Select One
A particle starts from rest with uniform acceleration a. Its velocity after n seconds is v. The displacement of the particle in the two seconds is :
A2v(n−1)nBv(n−1)nCv(n+1)nD2v(2n+1)n
A particle starts from rest and moves under constant acceleration in a straight line. Find the ratio of displacement (a) in successive second and (b) in successive time interval t0.
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
View SolutionA particle is projected vertically upwards from ground with an initial speed of 57m/s .If acceleration due to gravity is taken to be equal to 10m/s2 ,then the displacement of the particle in the sixth second of its motion will be?
View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration 4/3m/s2 ,in the third-second is
View SolutionA particle starts from rest, moving in a straight line with a time varying acceleration (inm/s2):a=30−152√t, where time is in seconds . The displacement of the particle in 4 seconds is .
View Solution