The converse of 'If x is zero then we cannot divide by x' is

A

If we cannot divide by x, then x is zero

B

If we cannot divide by x, then x is not zero

C

If x is not zero then we divide by x

D

None.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for The converse of 'If x is zero then we cannot divide by x' is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSMATHEMATICAL REASONING

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In the conversion of
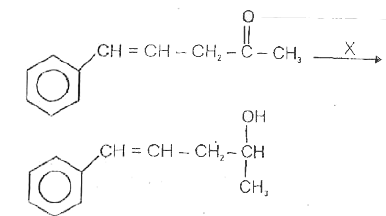
    ocr_image
    X is

    AH2/Pt
    BZn−Hg/HCl
    CLi/NH3
    DNaBH4

  • The converse of the statement ''If x>y, then x+a>y+a'' is

    AIf x<y, then x+a<y+a
    BIf x+a>y+a, then x>y
    Cif x<y, then x<y+a
    DIf x>y, then x+a<y+a

  • The converse of the statement "If a < b then x + a < x + b ", is

    AIf a > b then x + a < x + b
    BIf a ≥ b then x + a ≥ x + b
    CIf x + a < x + b then a < b
    DIf x + a ≥ x + b then a ≥ b