A: बामर श्रैणी, वैधुतचुम्बकीय स्पेक्ट्रम के दृश्य क्षेन्न में पड़ती है ।
R: 1λ=R[122−1n2] जहाँ n=3,4,5
A और R दोनों सत्य हैं और R , A की सही व्याख्या हैं।
A और R दोनों सत्य हैं परन्तु R , A की सही व्याख्या नहीं हैं।
A सत्य है परन्तु R असत्य हैं।
A और R दोनों असत्य हैं।
The correct Answer is:B
जब, n = 3 तो λ=6563Å और जब n=∞ तो λ=3646Å
(दृश्य क्षेत्र 3900Å से 7800Å तक है )
Topper's Solved these Questions
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (पूर्णांक उत्तर वाले प्रश्न )
7 Videos
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (सत्य या असत्य )
31 Videos
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (कॉलम मिलाना)
7 Videos
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (रिक्त स्थान भरना )
15 Videos
- परमाणुBOOK - GRB PUBLICATION HINDICHAPTER - परमाणुEXERCISE - NCERT पाठ्यपुस्तक अभ्यास उत्तरो सहित
16 Videos
Similar Questions
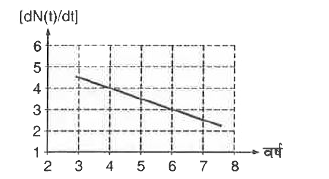
किसी रेडियोसक्रिय तत्व की अर्ध - आयु निकालने के लिए एक छात्र ln|dN(t)/dt| का एक t साथ ग्राफ़ बनता है [चित्र] यहाँ dN(t)/dt,t समय पर रेडियोसक्रिय क्षय की दर है। यदि इस तत्व के रेडियोसक्रिय नाभिकों की संख्या , 4.16 वर्षों के बाद p के घटक से कम हो जाती हो , तो p का मान है।
View Solutionकिसी परमाणु में इलेक्ट्रॉन की कुल ऊर्जा धनात्मक होती है ।
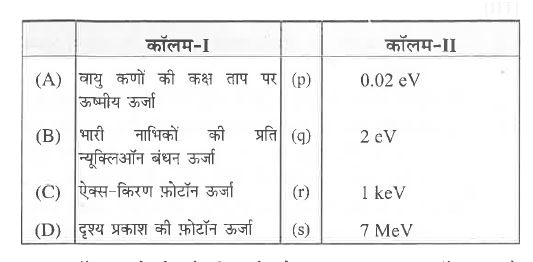
View Solutionकॉलम - I की सूची में दी गई भौतिक राशियों को कॉलम - II की सूची में यादृच्छिक रूप से दिए गए उनके मानों के साथ मिलाएँ।
View Solutionएकसमान धनात्मक आवेश Q (कूलॉम) वाली दो छोटी गेंदे एक स्टैण्ड से जुडी एक हुक के साथ L (मीटर ) लम्बी दो विधुतरोधी डोरियों से लटकाई जाती है। यह समूह उपग्रह द्वारा अंतरिक्ष में ले जाय जाता है जहाँ कोई गुरुत्व नहीं (भारहीनता की स्थिति ) है। दोनों डोरियों के बीच कोण .......... है और दोनों डोरियों में तनाव ........ न्यूटन है।
View Solutionटॉमसन मॉडल में परमाणु का साइज रदरफोर्ड मॉडल में परमाण्विक साइज से है। (बहु ज्यादा/कोई अलग नहीं/काफी कम)
View SolutionThe value of lim_(n rarr oo)(1*sum_(r=1)^(n)(r)+2*sum_(r=1)^(n-1)(r)+3sum_(r=1)^(n-2)(r)+....+n.1)/(n^(4))
View SolutionIf Δr=∣∣ ∣ ∣∣1r2r2nn2nn(n1)22n+1∣∣ ∣ ∣∣, then the value of n∑r=1Δr is
View SolutionIf Dr=∣∣ ∣ ∣∣r1n(n+1)22r−14n22r−152n−1∣∣ ∣ ∣∣, then the value of n∑r=1Dr, is
View SolutionStatement -2: n∑r=0(−1)rnCrr+1=1n+1
Statement-2: n∑r=0(−1)rnCrr+1xr=1(n+1)x{1−(1−x)n+1}
View SolutionProve that :
(i) n!r!=n(n−1)(n−2)...(r+1)
(ii) (n−r+1)⋅n!(n−r+1)!=n!(n−r)!
(iii) n!r!(n−r)!+n!(r−1)!(n−r+1)!=(n+1)!r!(n−r+1)!
View Solutionसिद्ध कीजिए कि -
(i) .nPr.nPr−2=(n−r+1)(n−r+2)
(ii) .n−1Pr+r⋅.n−1Pr−1=.nPr
(iii).2nPn=2n⋅{1⋅3⋅5⋅…⋅(2n−1)}
View SolutionIf Cr stands for .nCr=n!r!n−r!andn∑r=1r.C2r=λ for n≥2, then λ is divisible by
View Solution∣∣ ∣ ∣∣.n−1Cr−1.n−1Cr.n−1Cr+1.n−1Cr.n−1Cr+1.n−1Cr+2.nCr.nCr+1.nCr+2∣∣ ∣ ∣∣=
View Solution2≤r≤n के लिए (nr)+2(nr−1)+(nr−2) =
View SolutionLet for n∈N, f(n)=n∑r=0(−1)rCr2r+1(r+1)(r+2)
View Solution
