Question

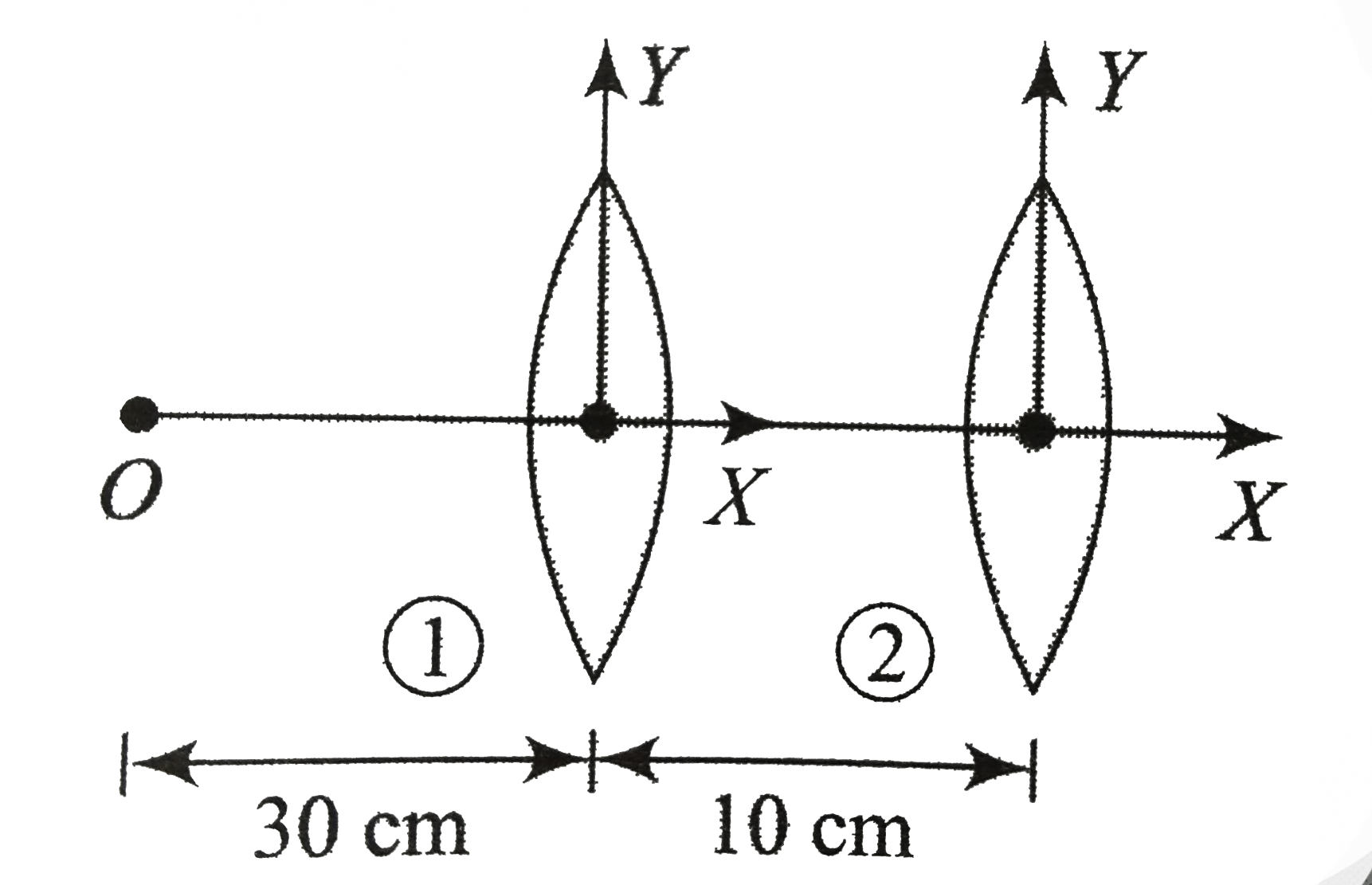
A convex lens of focal length 10 cm is coaxially placed near a concave lens. The combination forms the image of an object placed, 50 cm away from the convex lens to a point 30 cm away from the concave lens. If the distance between the optical centres of both the lens is 10 cm. calculate the focal length of concave lens.

Explanation

To solve the problem step by step, we will use the lens formula and the information provided in the question.

Step 1: Understand the setup
We have a convex lens (F1 = +10 cm) and a concave lens (F2) placed 10 cm apart. An object is placed 50 cm from the convex lens, and the final image is formed 30 cm from the concave lens.

Step 2: Calculate the image distance for the convex lens
Using the lens formula:
\( \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \)
For the convex lens:
- Focal length \( f_1 = +10 \) cm
- Object distance \( u = -50 \) cm (negative as per sign convention)

Substituting the values:
\( \frac{1}{10} = \frac{1}{v_1} - \frac{1}{-50} \)
This simplifies to:
\( \frac{1}{10} = \frac{1}{v_1} + \frac{1}{50} \)
Rearranging gives:
\( \frac{1}{v_1} = \frac{1}{10} - \frac{1}{50} \)
Finding a common denominator (50):
\( \frac{1}{v_1} = \frac{5}{50} - \frac{1}{50} = \frac{4}{50} = \frac{2}{25} \)
Thus:
\( v_1 = \frac{25}{2} = 12.5 \text{ cm} \)
This means the image \( I_1 \) is located 12.5 cm from the convex lens.

Step 3: Determine the position of the image \( I_1 \) relative to the concave lens
Since the distance between the two lenses is 10 cm, the distance from the concave lens to the image \( I_1 \) is:
\( \text{Distance from concave lens to } I_1 = 12.5 \text{ cm} - 10 \text{ cm} = 2.5 \text{ cm} \)
So, \( I_1 \) is 2.5 cm to the left of the concave lens.

Step 4: Calculate the object distance for the concave lens
For the concave lens, the object distance \( u_2 \) is positive because \( I_1 \) acts as a virtual object:
\( u_2 = +2.5 \text{ cm} \)

Step 5: Use the lens formula for the concave lens
The final image is located 30 cm from the concave lens (on the same side as the object):
\( v_2 = -30 \text{ cm} \text{ (negative as per sign convention)} \)
Using the lens formula for the concave lens:
\( \frac{1}{f_2} = \frac{1}{v_2} - \frac{1}{u_2} \)
Substituting the values:
\( \frac{1}{f_2} = \frac{1}{-30} - \frac{1}{2.5} \)
Calculating \( \frac{1}{2.5} \):
\( \frac{1}{2.5} = \frac{2}{5} = 0.4 \)
Thus:
\( \frac{1}{f_2} = -\frac{1}{30} - 0.4 \)
Finding a common denominator (60):
\( \frac{1}{f_2} = -\frac{2}{60} - \frac{24}{60} = -\frac{26}{60} = -\frac{13}{30} \)
Therefore:
\( f_2 = -\frac{30}{13} \approx -2.31 \text{ cm} \)

Final Answer
The focal length of the concave lens is approximately \( -2.31 \) cm.

---