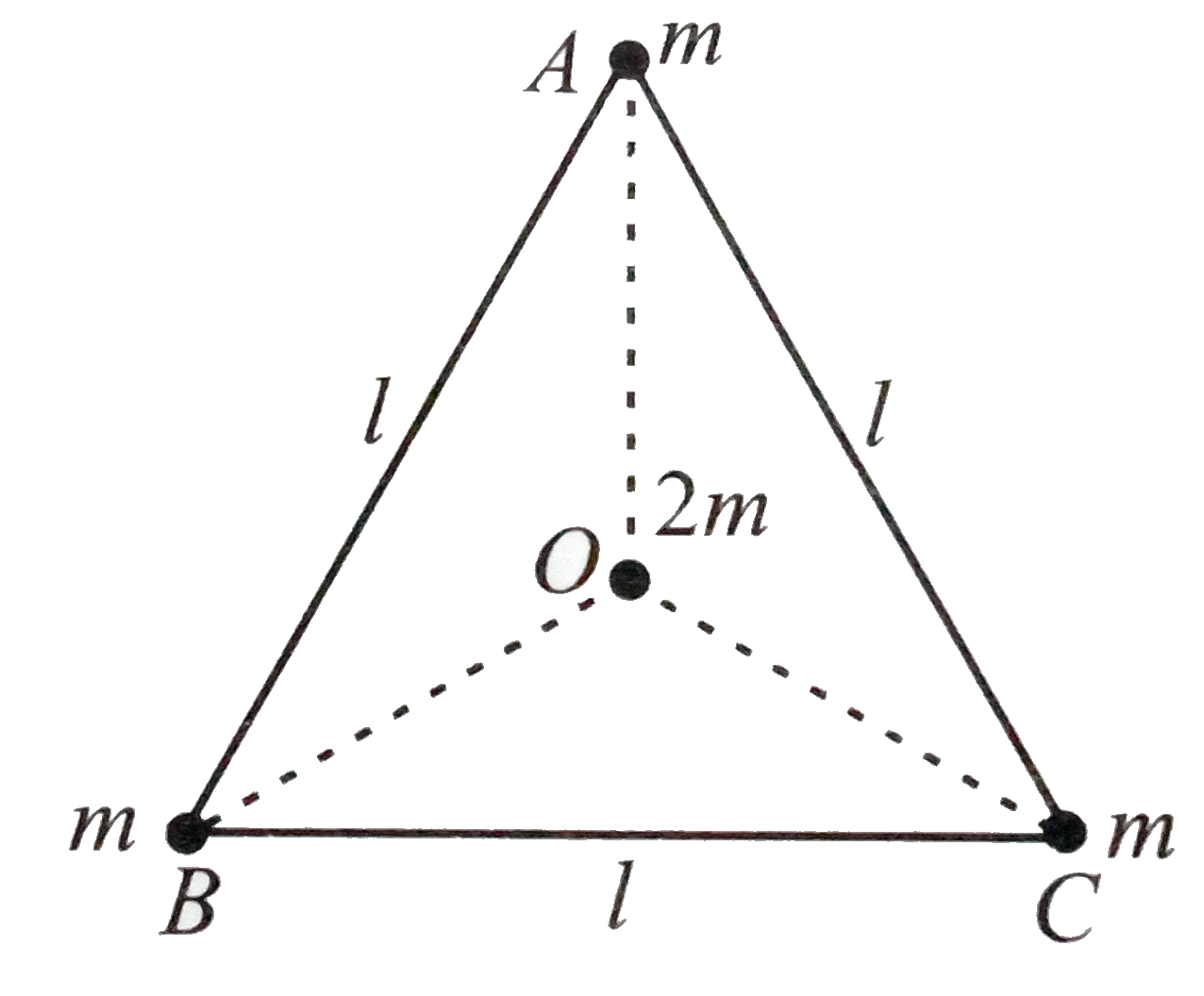
Three mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?

Video Solution

Text Solution

Verified by Experts

From $Δ O A D {\cos 30}^{\circ} = \frac{A D}{O A} = \frac{a / 2}{O A}$
$\frac{\sqrt{3}}{2} = \frac{a}{2 O A}$
$O A = \frac{a}{\sqrt{3}}$
Gravitational fields at O due to masses at A, B, C
$E_{1} = \frac{G m}{{(O A)}^{2}} = \frac{G m}{{(a / \sqrt{3})}^{2}} = \frac{3 G m}{a^{2}}$ along OA
$E_{2} = \frac{G m}{{(O B)}^{2}} = \frac{G m}{{(a / \sqrt{3})}^{2}} = \frac{3 G m}{a^{2}}$ along OB
$E_{3} = \frac{G m}{{(O C)}^{2}} = \frac{G m}{{(a / \sqrt{3})}^{2}} = \frac{3 G m}{a^{2}}$ OC
As the angle between $E_{1}$ and $E_{3}$ is $120^{\circ}$
$∴ E = \sqrt{E_{1}^{2} + E_{3}^{2} + 2 E_{1} E_{3} {\cos 120}^{\circ}}$
$= \frac{3 G M}{a^{2}}$ (along EM)
As E is equal and opposite to ${\vec{E}}_{2}$ , the resultant gravitational field at O is zero.
Total gravitational potential at O, $V = V_{1} + V_{2} + V_{3}$
$= - \frac{G m}{O A} - \frac{G m}{O B} - \frac{G m}{O C}$
$= - \frac{3 G m}{O A} (∵ O A = O B = O C = \frac{a}{\sqrt{3}})$
$= \frac{- 3 G m}{a / \sqrt{3}}$
$= - 3 \sqrt{3} \frac{G m}{a}$

Updated on:21/07/2023

Three particles each of mass $m$ are kept at the vertices of an euilateral triangle of side $L$ . The gravitational field at the centre due to these particle is
A $- \frac{3 G M}{L}$
B $- \frac{\sqrt{3} G M}{L}$
C $- \frac{3 \sqrt{3} G M}{L}$
D $- \frac{G M}{3 \sqrt{3} L}$
Three particles each of mass $m$ are kept at the vertices of an euilateral triangle of side $L$ . The gravitational field at the centre due to these particle is
Azero
B $\frac{3 G M}{L^{2}}$
C $\frac{9 G M}{L^{2}}$
D $\frac{2 G M}{L^{2}}$
Three particles each of mass $m$ are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
Azero
B $\frac{3 G M}{L^{2}}$
C $\frac{9 G M}{L^{2}}$
D $\frac{12 G M}{\sqrt{3} L^{2}}$