A particle is moving in a circular path of radius a under the action of an attractive potential U=−k2r2. Its total energy is :
Zero
−32ka2
−k4a2
k2a2
The correct Answer is:C
U=−K2r2
Force can be calculated from potential energy as follows :
F=dUdr=−K2(−2r3)=−Kr3
Negative sign indicates that it is central force which acts as centripetal force for the circular motion of particle . Hence we ca write the following equation using circular dynamics :
Kr3=mv2r⇒mv2=Kr2
⇒K.E=12mv2=K2r2
Total energy T.E=P.E+K.E=0
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (JEE (Advanced) for IIT Entrance)
7 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (C. Multiple Choice Questions)
16 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (B. Multiple Choice Questions)
46 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
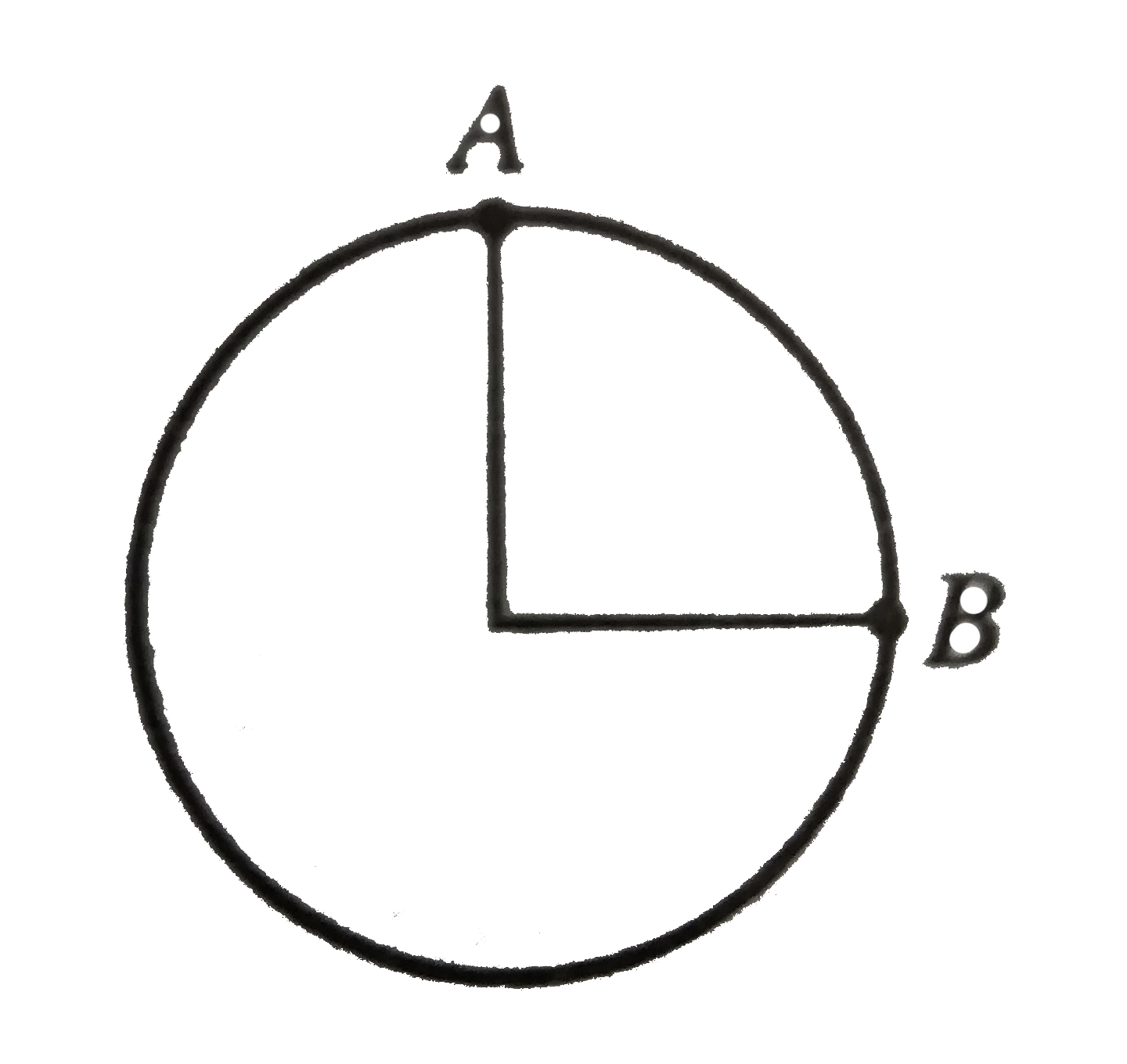
View SolutionIF a particle of mass m is moving in a horizontal circle of radius r with a centripetal force (−Kr2) , then its total energy is
View Solution
Knowledge Check
A particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
A→F.→v=0B→F.→c>0C→F.→v<0D→F.→v≥0A particle is moving along a circular path of radius of R such that radial acceleration of particle is proportional to t2 then
ASpeed of particle is constantBMagnitude of tangential acceleration of particle is constantCSpeed of particle is proportional to timeDMagnitude of tangential acceleration is variableA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
A√rFmB√FrC√FmrD√Fmr
A particle is moving in a circle of radius r under the action of a force F=αr2 which is directed towards centre of the circle.Total mechanical enery (kinetic energy+potential energy)of the particle is (take potential energy=0 for r=0)
View SolutionA particle of mass 'm' moves with a constant speed along a circular path of radius r under the action of a force F .Its speed is given by
View SolutionA particle of mass m moves in a circular path of radius r, under the action of force which delivers it constant power p and increases its speed. The angular acceleration of particle at time (t) is proportional
View SolutionA particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance r. The speed of the particle is
View SolutionA particle moves in a circular orbit under the action of a central attractive force which is inversely proportional to the distance 'r' . The speed of the particle is
View Solution
