A platform having no mass is kept on a light elastic spring . When a small particle of 0.1 kg is dropped on this spring from a height of 0.50 m , the spring is compressed by 0.02 m . From which height the particle should be dropped to produce a compression of 0.05 m ?
To solve the problem, we will use the work-energy principle, which states that the work done on an object is equal to the change in its kinetic energy.
1. Understand the Problem: We have a particle of mass m=0.1kg dropped from a height h onto a spring. The spring compresses by x meters. We need to find the height h from which the particle should be dropped to produce a compression of 0.05m.
2. Initial Conditions:
- When the particle is dropped from a height of 0.50m, the spring compresses by 0.02m.
- The gravitational force acting on the particle is mg, where g=10m/s2.
3. Apply Work-Energy Principle:
- The work done by gravity when the particle falls is equal to the potential energy lost, which is mgh.
- The work done against the spring when it compresses is given by 12kx2, where k is the spring constant.
4. Set Up the Equation for the First Case:
- For the first drop (height 0.50m and compression 0.02m):
mgh+x=12kx2
Substituting the known values:
0.1⋅10⋅0.50+0.02=12k(0.02)2
Simplifying:
0.5+0.02=12k(0.0004)
0.52=0.0002k(Equation 1)
5. Set Up the Equation for the Second Case:
- For the second drop (unknown height h and compression 0.05m):
mgh+0.05=12k(0.05)2
Substituting the known values:
0.1⋅10⋅h+0.05=12k(0.0025)
Simplifying:
h+0.05=0.00125k(Equation 2)
6. Divide Equation 2 by Equation 1:
h+0.050.52=0.00125k0.0002k
The k cancels out:
h+0.050.52=0.001250.0002=6.25
7. Solve for h:
h+0.05=6.25⋅0.52
h+0.05=3.25
h=3.25−0.05=3.20m
Final Answer:
The particle should be dropped from a height of 3.20 meters to produce a compression of 0.05 m in the spring.
- When the particle is dropped from a height of 0.50m, the spring compresses by 0.02m.
- The gravitational force acting on the particle is mg, where g=10m/s2.
- The work done by gravity when the particle falls is equal to the potential energy lost, which is mgh.
- The work done against the spring when it compresses is given by 12kx2, where k is the spring constant.
- For the first drop (height 0.50m and compression 0.02m):
mgh+x=12kx2
Substituting the known values:
0.1⋅10⋅0.50+0.02=12k(0.02)2
Simplifying:
0.5+0.02=12k(0.0004)
0.52=0.0002k(Equation 1)
- For the second drop (unknown height h and compression 0.05m):
mgh+0.05=12k(0.05)2
Substituting the known values:
0.1⋅10⋅h+0.05=12k(0.0025)
Simplifying:
h+0.05=0.00125k(Equation 2)
h+0.050.52=0.00125k0.0002k
The k cancels out:
h+0.050.52=0.001250.0002=6.25
h+0.05=6.25⋅0.52
h+0.05=3.25
h=3.25−0.05=3.20m
The particle should be dropped from a height of 3.20 meters to produce a compression of 0.05 m in the spring.
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (A. Multiple Choice Questions)
Explore 29 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (B. Multiple Choice Questions)
Explore 46 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Revision Exercise (Long Answer Questions)
Explore 9 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
A massless platform is kept on a light elastic spring as shown in figure. When a small stone of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the spring compresses by 0.01m. From what height should the stone be droppped to cause a compression of 0.04m in the spring ?
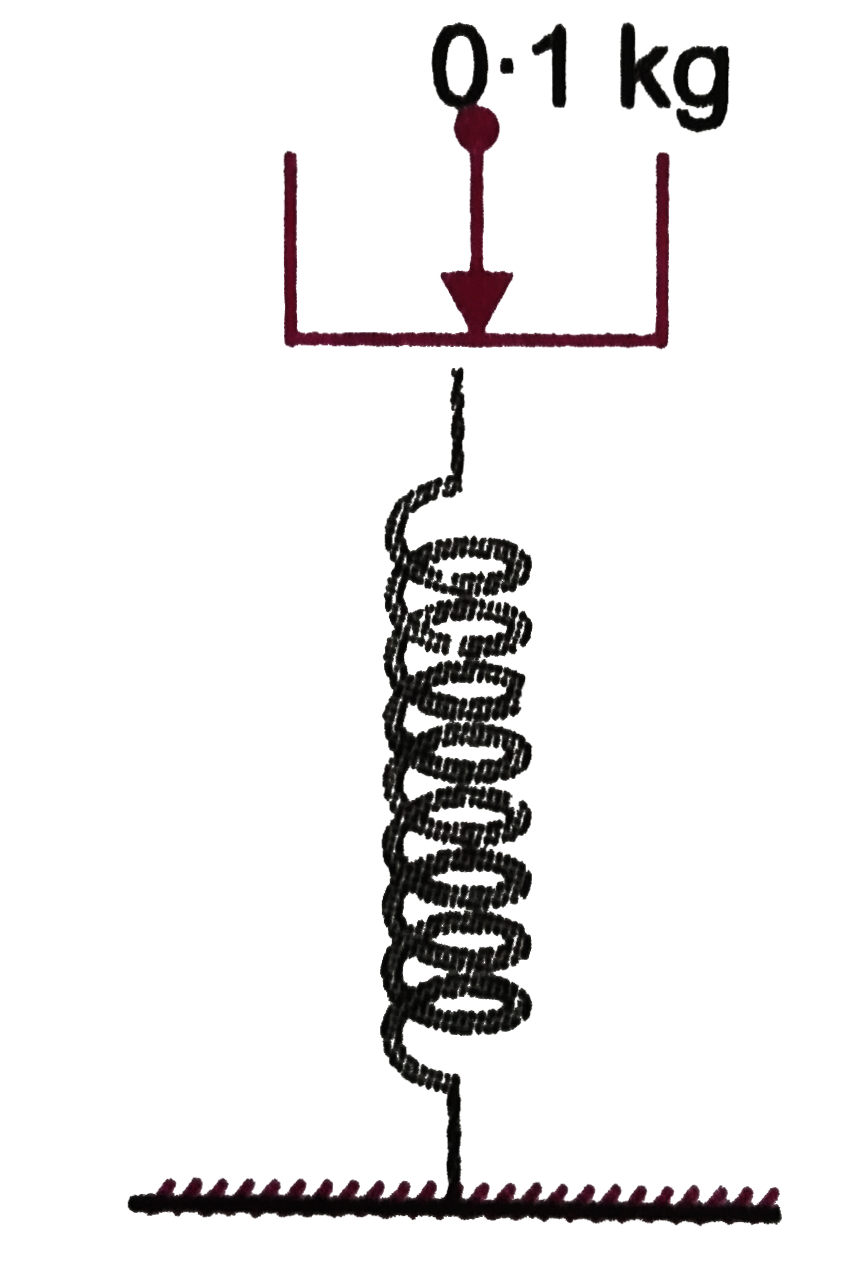
View SolutionGiven figure shows a massless platform kept on a light elastic spring attached to ground from one end .
A small particle of mass 0.2 kg is dropped on the paltform from a height of 0.26 m , which causes a compression of 0.01 m in the spring . Calculate the height from which the particle must be dropped in order to cause a compressin of 0.05 m .
View Solution
Knowledge Check
A massless platform is kept on a light elastic spring, as shown in the figure. When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m?
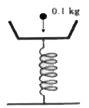 A0.96 mB2.96 mC3.96 mD0.48 m
A0.96 mB2.96 mC3.96 mD0.48 mThe two masses m1 and m2 are joined by a spring as shown. The system is dropped to the ground from a height. The spring will be
 AStreched when m2>m1BCompressed when m2<m1Cneither compressed not stretched only when m1=m2Dneither compressed not stretched regardless of the values of m1 and m2.
AStreched when m2>m1BCompressed when m2<m1Cneither compressed not stretched only when m1=m2Dneither compressed not stretched regardless of the values of m1 and m2.A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1
In figure a spring with k=168N/m is in its relaxed length and is at the top of a frictionless incline of angle θ=37∘. The lower end of the incline is at distance D = 1 m from the end of the spring. A small blcok of mass 2 kg is pushed against the spring until the spring is compressed by 0.2 m and released from rest.
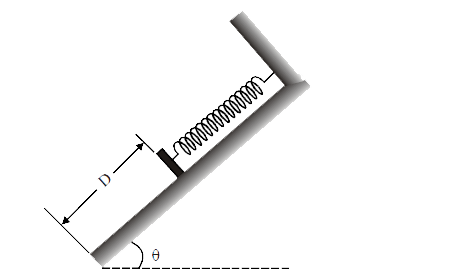
What is the speed of the block when it reaches the lower end of the incline?
View SolutionA spring gets compressed when a body of mass 5 g is dropped on it from a height of 2 m . Calculate the maximum distance s through whichthe spring is compressed. The force constant of spring is 100Nm−1 .
View SolutionA block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View SolutionWhen a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
View Solution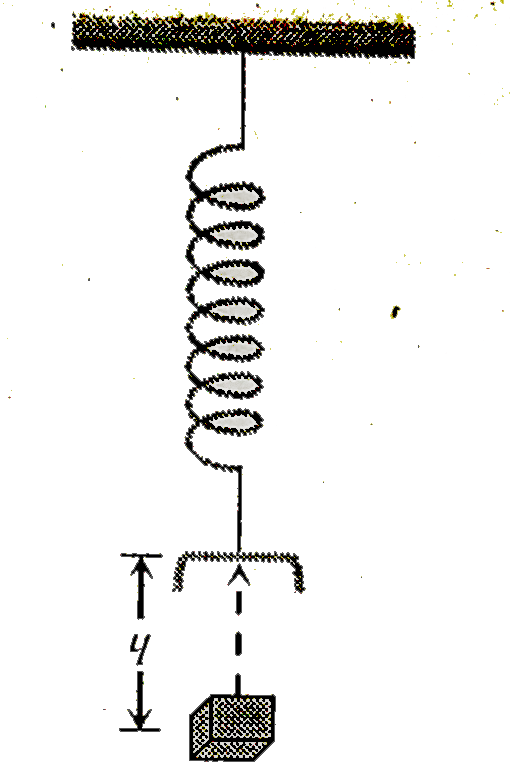
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View Solution

