From the given isothem for one mole of an ideal gas, which follows Boyle's law, what wil be the value of temperature? (R 0.0821 litre atm ).

A
B
1220 K
C
947 K
D
48 K
Text Solution
The correct Answer is:B
|
Topper's Solved these Questions
- GASEOUS STATEBook:FIITJEEChapter:GASEOUS STATEExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II
Explore 20 Videos
- GASEOUS STATEBook:FIITJEEChapter:GASEOUS STATEExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL-II COMPREHENSION-I
Explore 5 Videos
- GASEOUS STATEBook:FIITJEEChapter:GASEOUS STATEExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL-2
Explore 9 Videos
- ENVIRONMENTAL CHEMISTRYBook:FIITJEEChapter:ENVIRONMENTAL CHEMISTRYExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) LEVEL -II (MULTIPLE CORRECT QUESTIONS)
Explore 20 Videos
- GENERAL ORGANIC CHEMISTRYBook:FIITJEEChapter:GENERAL ORGANIC CHEMISTRYExercise:SINGLE INTEGER ANSWER TYPE QUESTIONS
Explore 14 Videos
Similar Questions
Knowledge Check
For the given isotherm for one mole of an ideal gas, which follows Boyle's law, what will be the value of temperature (R = 0.0821 (L atm/mol/K))
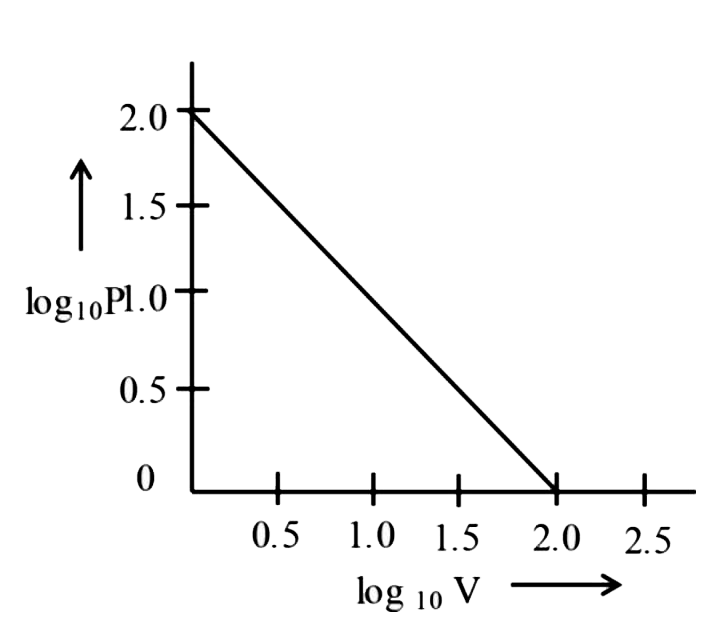 A8.2×10−4 KB1220 KC947 KD18 K
A8.2×10−4 KB1220 KC947 KD18 KFor the given isotherm (P in atm and V in L) for one mole of an ideal gas, which follows Boyle's law, what will be the approx value of temperature ? (R=0.0821Latm/molK)
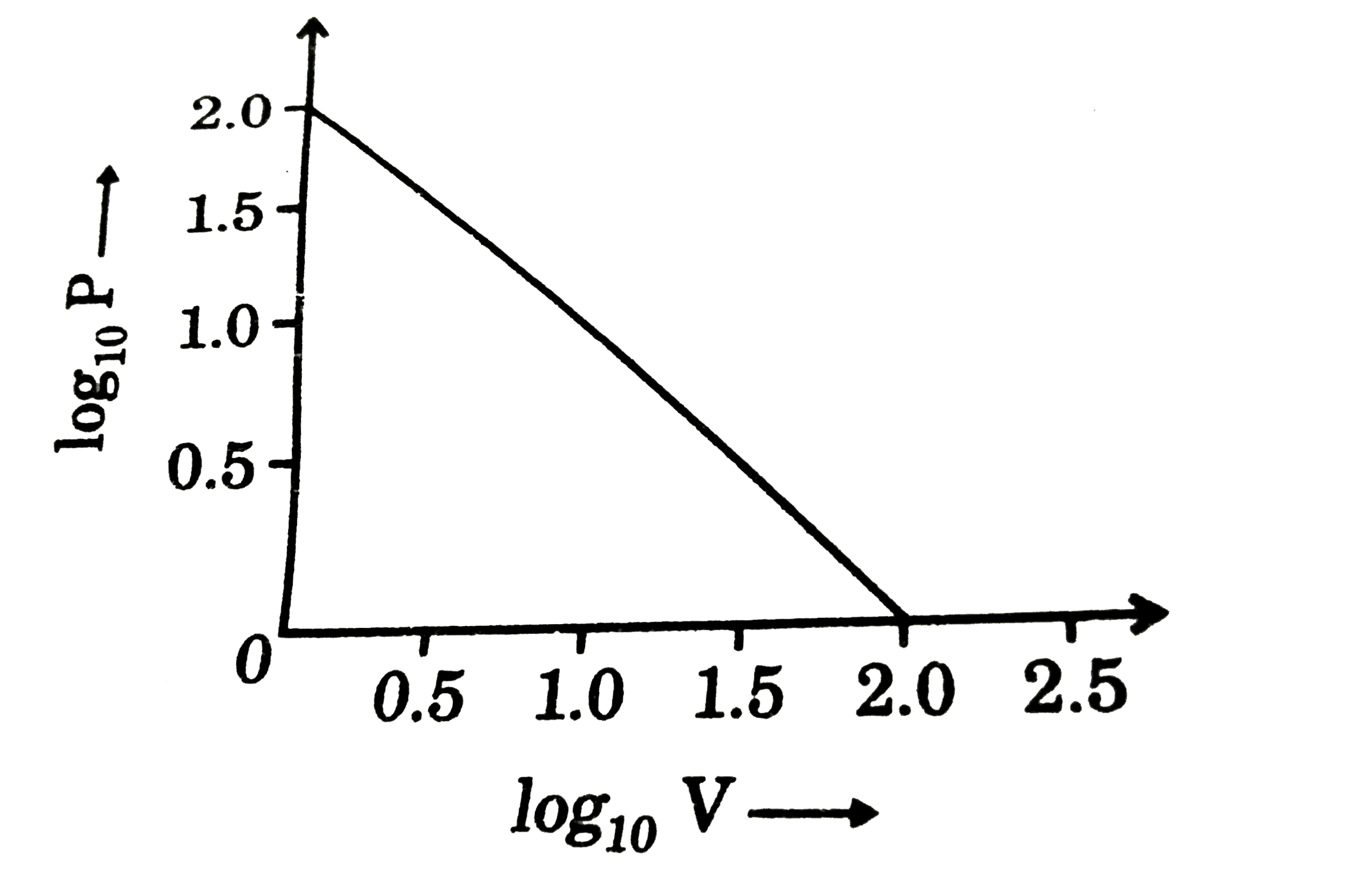 A8.2×10−4KB1220KC947KD48K
A8.2×10−4KB1220KC947KD48KIf two moles of an ideal gas at 500 K occupies a volume of 41 litres, the pressure of the gas is (R=0.082LatmK−1mol−1)
A2 atmB3 atmC4 atmD5 atm
Work done during isothermal expansion of one mole of an ideal gas from 10 atm to 1atm at 300 k is
View SolutionUnder what conditions will a pure sample of an ideal gas not only exhibit a pressure of 1atm but also a concentration of 1mollitre−1
[R=0.082 iltre atm mol−1K−1]
View SolutionThe volume of 2.8g of CO at 27∘C and 0.821atm pressure is (R=0.0821 lit. atm mol−1K−1)
View SolutionWork done during isothermal expansion of one mole of an ideal gas from 10 atm to 1atm at 300 k is
View SolutionKinetic energy of 0.3 mole of 'He' gas in a container of maximum capacity of 4 litre at 5 atm, must be :
(R=0.821atm litre mol−1K−1)
View Solution

