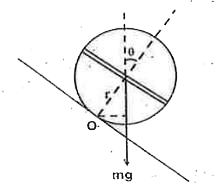
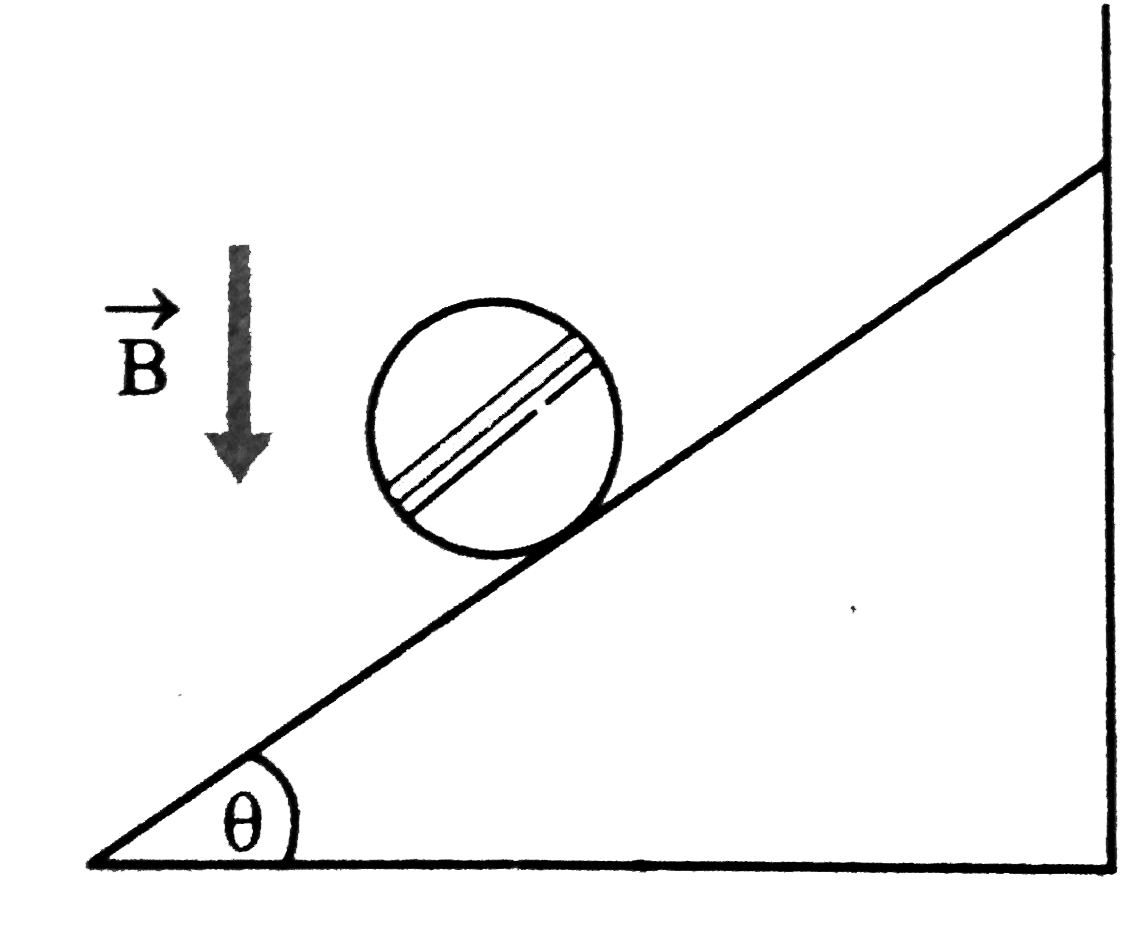
In Fig. a coil of single turn is wound on a sphere of radius r and mass m. The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equilibrium, the value of B is [Current in the coil is i]

$\frac{m g}{π r}$

$\frac{m g sin θ}{π i}$

$\frac{m g r sin θ}{π i}$

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
A $\frac{7}{6}$
B $\frac{5}{4}$
C $\frac{3}{2}$
Ddepends on angle of inclination
A solid sphere of mass m rolls without slipping on an inclined plane of inclination $θ$ . The linear acceleration of the sphere is
A $\frac{7}{5} g sin θ$
B $\frac{2}{7} g sin θ$
C $\frac{3}{7} g sin θ$
D $\frac{5}{7} g sin θ$
P is a solid sphere and Q is a hollow sphere both having the same mass and radius .If they roll down from the top of an inclined plane , on reaching the bottom .
AVelocity of P is more
BVelocity of Q is more
CVelocity of P = velocity of Q
DNone