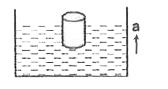
The period of oscillation of the wooden cylinder is Tc in the liquid. If the liquid accelerates up with an acceleration a time new time period of oscillation will be T say Then TT0 is equal to

1:1
g:a
√g:(g+a)
none of these
The correct Answer is:C
Time period will remain same in both the cases,
Constant force will only charge its equilibrium position
∴TT0=1s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Subjective) (Level)
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Subjective) (Level-II & III)
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix Match Type
11 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
Similar Questions
The time period of simple pendulum inside a stationary lift is T. If lift starts accelerating upwards with the acceleration of g/2, then the new time period of the simple pendulum will be
View SolutionA pendulum is suspended in a lit and its period of oscillation is T0 when the lift is stationary.
(i) What will be the period T of oscillation of pendulum, if the lift begins to accelerates downwards with an acceleration equal to 3g4 ?
(ii) What must be the accleration of the lift for the period of oscillation of the pendulum to be T02 ?
View Solution
Knowledge Check
A man measures the period of a simple pendulum inside a stationary lift and find it be T. If the lift accelerates downwards with an acceleration of g/3, then the period of the pendulum will be
A√2TBT√2C√32TDT3A man measures time period of a pendulum (T) in stationary lift. If the lift moves upward with acceleration g4, then new time period will be
A2T√5B√5T2C√52TD2√5TThe time period of a simple pendulum measured inside a stationary lift is found to be T . If the lift starts accelerating upwards with an acceleration g/3, the time period is
AT√3BT√3/2CT/√3DT/3
A pendulum suspended from the ceiling of an elevator at rest has a time period of oscillation equal to T1. When the elevator moves up with an acceleration a, the time period becomes T2 and when the elevator moves down with an acceleration a, its time period becomes T3, then find the expression for T1 in terms of T2 and T3.
View SolutionThe period of oscillation of a spring pendulum is T. If the spring is cut into four equal parts, then find the time period corresponding to each part.
View SolutionTime period of a simple pendulum of length L is T1 and time period of a uniform rod of the same length L pivoted about an end and oscillating in a vertical plane is T2. Amplitude of osciallations in both the cases is small. Then T1T2 is
View SolutionA pendulum suspended from the ceiling of a train has time period T when the train is at rest .When the train is accelerating with a uniform acceleration ,the time period will
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
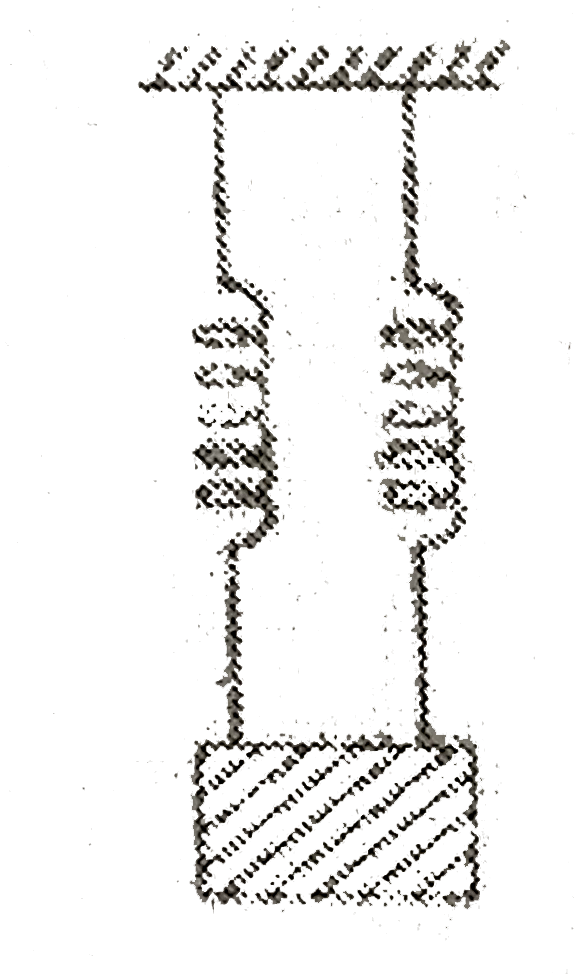
View Solution
