An iron pillar has some part n the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of base of cone , as well as cylinder is 21 cm . The cylindrical part is 80 cm high and conical part is 16 cm high . Find the weight of the pillar , if 1cm3 of iron weighs 8.45 g :
999.39 kg
111 kg
1001 kg
989 kg
The correct Answer is:A
To solve the problem of finding the weight of the iron pillar, we need to calculate the total volume of the pillar, which consists of a cylindrical part and a conical part, and then use the density of iron to find the weight. Here’s the step-by-step solution:
Step 1: Identify the dimensions
- Radius of the base (r) = 21 cm
- Height of the cylindrical part (h_cylinder) = 80 cm
- Height of the conical part (h_cone) = 16 cm
Step 2: Calculate the volume of the cylindrical part
The formula for the volume of a cylinder is:
Vcylinder=πr2h
Substituting the values:
Vcylinder=π×(21)2×80
Step 3: Calculate the volume of the conical part
The formula for the volume of a cone is:
Vcone=13πr2h
Substituting the values:
Vcone=13π×(21)2×16
Step 4: Combine the volumes
The total volume of the pillar is the sum of the volumes of the cylinder and the cone:
Vtotal=Vcylinder+Vcone
Step 5: Factor out common terms
We can factor out π and 212:
Vtotal=π×(21)2×(80+13×16)
Step 6: Calculate the expression inside the parentheses
Calculate 80+13×16:
13×16=163
Convert 80 to a fraction:
80=2403
So,
80+163=240+163=2563
Step 7: Substitute back into the volume formula
Now we have:
Vtotal=π×(21)2×2563
Step 8: Calculate 212
212=441
Step 9: Substitute and calculate the total volume
Vtotal=π×441×2563
Using π≈227:
Vtotal=227×441×2563
Step 10: Simplify the calculation
Calculate:
Vtotal=22×441×25621
Step 11: Calculate the weight of the pillar
The weight of the pillar can be found by multiplying the volume by the weight of 1 cm³ of iron:
Weight = Volume × Density
Weight=Vtotal×8.45
Step 12: Convert weight to kilograms
Since the weight is calculated in grams, convert it to kilograms by dividing by 1000.
Final Calculation
After calculating all the above steps, we find that the weight of the iron pillar is approximately 999.3984 kg.
- Radius of the base (r) = 21 cm
- Height of the cylindrical part (h_cylinder) = 80 cm
- Height of the conical part (h_cone) = 16 cm
The formula for the volume of a cylinder is:
Vcylinder=πr2h
Vcylinder=π×(21)2×80
The formula for the volume of a cone is:
Vcone=13πr2h
Vcone=13π×(21)2×16
The total volume of the pillar is the sum of the volumes of the cylinder and the cone:
Vtotal=Vcylinder+Vcone
We can factor out π and 212:
Vtotal=π×(21)2×(80+13×16)
Calculate 80+13×16:
13×16=163
Convert 80 to a fraction:
80=2403
So,
80+163=240+163=2563
Now we have:
Vtotal=π×(21)2×2563
212=441
Vtotal=π×441×2563
Vtotal=227×441×2563
Calculate:
Vtotal=22×441×25621
The weight of the pillar can be found by multiplying the volume by the weight of 1 cm³ of iron:
Weight = Volume × Density
Weight=Vtotal×8.45
Since the weight is calculated in grams, convert it to kilograms by dividing by 1000.
After calculating all the above steps, we find that the weight of the iron pillar is approximately 999.3984 kg.
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING
18 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 1)
55 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weighs 7.8 grams.
View SolutionAn iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find
(i) The volume of iron used
(ii) The weight of pillar, if 1 cm3 of iron weighs 10g.
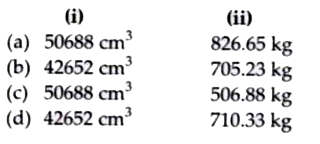
View Solution
Knowledge Check
An iron pillar has some part n the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of base of cone , as well as cylinder is 21 cm . The cylindrical part is 80 cm high and conical part is 16 cm high . Find the weight of the pillar , if 1cm3 of iron weighs 8.45 g :
A999.39 kgB111 kgC1001 kgD989 kgAn iron pillar has some part in the from of right circular cylinder and the remaining in the from of a right circular cone .The radius of the base of each of the cone and the cylinder is 8 cm . The cylindrical part is 240 cm hight and the conical part is 36 cm hight .Find the weight of the pillar if 1 cubic centimetre of iron weighs 7.5 g .
A480. 16 kgB380.16kgC580. 16 kgD680. 16 kgThe volume of a right circular cylinder, 14 cm in height is equal to that of a cube whose edge is 11 cm. The radius of the base of the cylinder is (a) 5.2 cm (b) 5.5 cm (c) 11 cm (d) 22 cm
A5.2 cmB5.5 cmC11 cmD22 cm
An iron pillar consists of a cylindrical portion of 2.8m. height and 20cm. in diamea cone of 42cm. height surmounting it. Find the weight of the pillar if 1cm3 of iron weights 7.5g.
View SolutionA iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm heigh is surmounting it. Find the weight of the pillar, given that 1cm3 of iron weight 7.5 g
View SolutionVolume of a right circular cylinder of height 21 cm and base radius 5 cm is
View SolutionFind the volume of a right circular cylinder of length 80 cm and diameter of the base 14 cm.
View SolutionVolume of a right circular cylinder of height 21 cm and base radius 5 cm is :
View Solution
