A, B and C are situated at the bank of river which is flowing at a constant rate. B is at an equal distance with A and C. A swimmer Avinash takes 10 h to swim from A to B and B to A .Also ,he takes 4 h to swim from A to C. What is the ratio of speed of Avinash in still water and speed of stream?
5:3
3:5
2:5
1:2
The correct Answer is:A
To solve the problem, we need to establish the relationship between the speeds of Avinash in still water and the speed of the stream. Let's denote:
- Speed of Avinash in still water = x km/h
- Speed of the stream = y km/h
Step 1: Understand the distances and times
Avinash takes 10 hours to swim from A to B and back to A. This means the total time for the round trip from A to B is 10 hours.
Step 2: Calculate the effective speed from A to B
Let the distance from A to B be d km. The effective speed when swimming downstream (from A to B) is (x + y) km/h, and the effective speed when swimming upstream (from B to A) is (x - y) km/h.
The time taken to swim downstream from A to B is:
TimeAB=dx+y
The time taken to swim upstream from B to A is:
TimeBA=dx−y
Since the total time for the round trip is 10 hours:
dx+y+dx−y=10
Step 3: Simplify the equation
To simplify, we can combine the fractions:
d(x−y)+d(x+y)(x+y)(x−y)=10
This simplifies to:
2dx(x+y)(x−y)=10
Step 4: Rearranging the equation
Multiplying both sides by (x + y)(x - y):
2dx=10(x2−y2)
2dx=10x2−10y2
Dividing everything by 2:
dx=5x2−5y2
Rearranging gives us:
5x2−dx−5y2=0 (Equation 1)
Step 5: Calculate the effective speed from A to C
Avinash takes 4 hours to swim from A to C. Since B is equidistant from A and C, let the distance from A to C also be d km.
The effective speed when swimming downstream from A to C is still (x + y) km/h, and the time taken is:
dx+y=4
This implies:
d=4(x+y) (Equation 2)
Step 6: Substitute Equation 2 into Equation 1
Substituting d from Equation 2 into Equation 1:
5x2−4(x+y)x−5y2=0
Expanding gives:
5x2−4x2−4xy−5y2=0
This simplifies to:
x2−4xy−5y2=0
Step 7: Factor the quadratic equation
Factoring gives:
(x−5y)(x+y)=0
This gives us two possible solutions:
1. x−5y=0 → x=5y
2. x+y=0 → Not possible since speeds cannot be negative.
Step 8: Find the ratio
From x=5y, the ratio of the speed of Avinash in still water to the speed of the stream is:
xy=5
Final Answer
The ratio of the speed of Avinash in still water to the speed of the stream is 5:1.
- Speed of the stream = y km/h
Avinash takes 10 hours to swim from A to B and back to A. This means the total time for the round trip from A to B is 10 hours.
Let the distance from A to B be d km. The effective speed when swimming downstream (from A to B) is (x + y) km/h, and the effective speed when swimming upstream (from B to A) is (x - y) km/h.
TimeAB=dx+y
TimeBA=dx−y
dx+y+dx−y=10
To simplify, we can combine the fractions:
d(x−y)+d(x+y)(x+y)(x−y)=10
This simplifies to:
2dx(x+y)(x−y)=10
Multiplying both sides by (x + y)(x - y):
2dx=10(x2−y2)
2dx=10x2−10y2
Dividing everything by 2:
dx=5x2−5y2
Rearranging gives us:
5x2−dx−5y2=0 (Equation 1)
Avinash takes 4 hours to swim from A to C. Since B is equidistant from A and C, let the distance from A to C also be d km.
dx+y=4
This implies:
d=4(x+y) (Equation 2)
Substituting d from Equation 2 into Equation 1:
5x2−4(x+y)x−5y2=0
Expanding gives:
5x2−4x2−4xy−5y2=0
This simplifies to:
x2−4xy−5y2=0
Factoring gives:
(x−5y)(x+y)=0
This gives us two possible solutions:
1. x−5y=0 → x=5y
2. x+y=0 → Not possible since speeds cannot be negative.
From x=5y, the ratio of the speed of Avinash in still water to the speed of the stream is:
xy=5
The ratio of the speed of Avinash in still water to the speed of the stream is 5:1.
Topper's Solved these Questions
- BOATS AND STREAMS BOOK - ARIHANT SSCCHAPTER - BOATS AND STREAMS EXERCISE - EXERCISE BASE LEVEL QUESTIONS
27 Videos
- BAR CHARTBOOK - ARIHANT SSCCHAPTER - BAR CHARTEXERCISE - Higher Skill Level Questions
20 Videos
- CI/SI/INSTALMENTSBOOK - ARIHANT SSCCHAPTER - CI/SI/INSTALMENTSEXERCISE - EXERCISE (LEVEL - 2)
23 Videos
Similar Questions
Boat A travels downstream from Point X to Point Y in 3 hours less than the time taken by Boat B travel upstream from Point Y to Point Z. The distance between X and Y is 20 km, which is half of the distance between Y and Z. The speed of Boat B in still water is 10 km/h and the speed of Boat A in still water is equal to the speed of Boat B upstream What is the speed of Boat A in Still water? (Consider the speed of the current to be the same.) a. 10 km/h b. 16 km/h c. 12 km/h d. 8 km/h
View SolutionA boat can move at 5 km/h in still water(i.e, when water is not flowing).The speed of stream of the river is 1 km/h .A boat takes 80 min to go from a point A to another point B and return to the same point. What is the ratio of downstream speed and upstream speed?
View Solution
Knowledge Check
A and B are two fixed spots in a river in which water has a steady sped vw. A person who can swim with a speed v relative to water swims from A to B and back to A alomg shortest path. If the
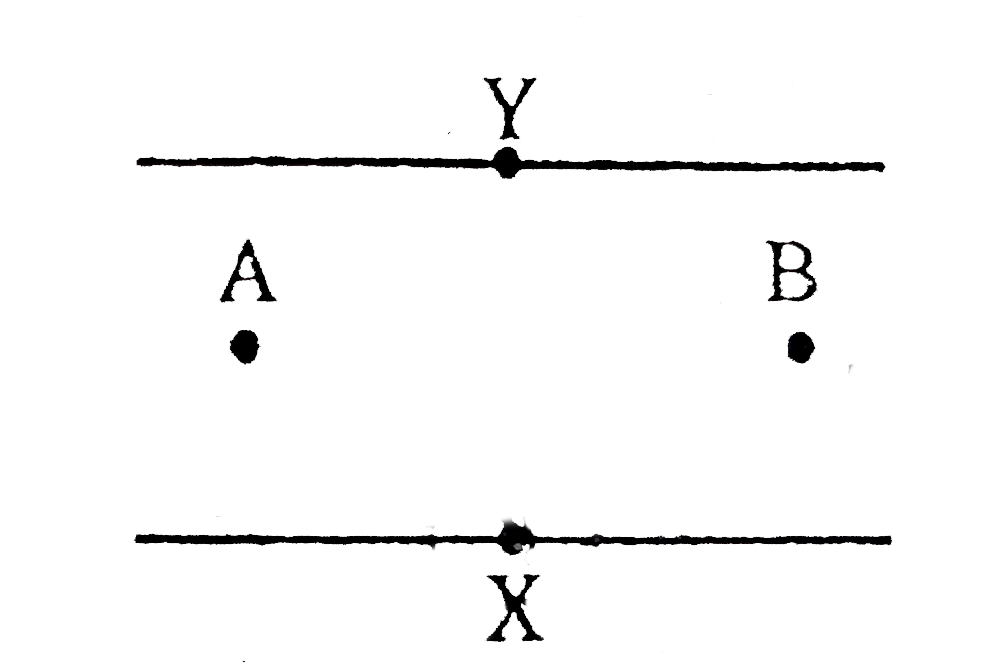
water is still, the person will take a time 30 minute in swimming from A to B and back to A along the shortes path. But we know that water is acually not still. The person also knows the technique of just flowing with water without exerting his own effort. Using this technique, i.e., just being carried with water, he takes a time 20 minute in moving from A to B. As shown, X and Y are two places directly oppsite to each other on oppsite banks. Assuming that width of the river is the same as the distance A and B, answer these questions. (assume v>vw)
Choose the correct option(s) :A12 minB15 minC8 minD25 minA and B are two fixed spots in a river in which water has a steady sped vw. A person who can swim with a speed v relative to water swims from A to B and back to A alomg shortest path. If the
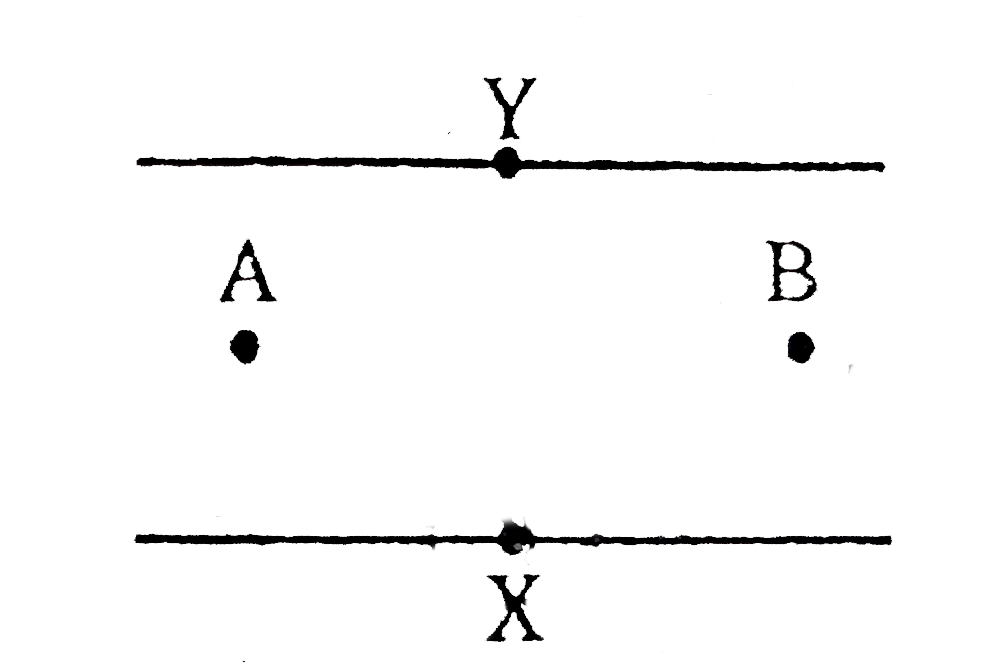
water is still, the person will take a time 30 minute in swimming from A to B and back to A along the shortes path. But we know that water is acually not still. The person also knows the technique of just flowing with water without exerting his own effort. Using this technique, i.e., just being carried with water, he takes a time 20 minute in moving from A to B. As shown, X and Y are two places directly oppsite to each other on oppsite banks. Assuming that width of the river is the same as the distance A and B, answer these questions. (assume v>vw)
Choose the correct option(s) :A60 minB45 minC30 minD12 minA and B are two fixed spots in a river in which water has a steady sped vw. A person who can swim with a speed v relative to water swims from A to B and back to A alomg shortest path. If the
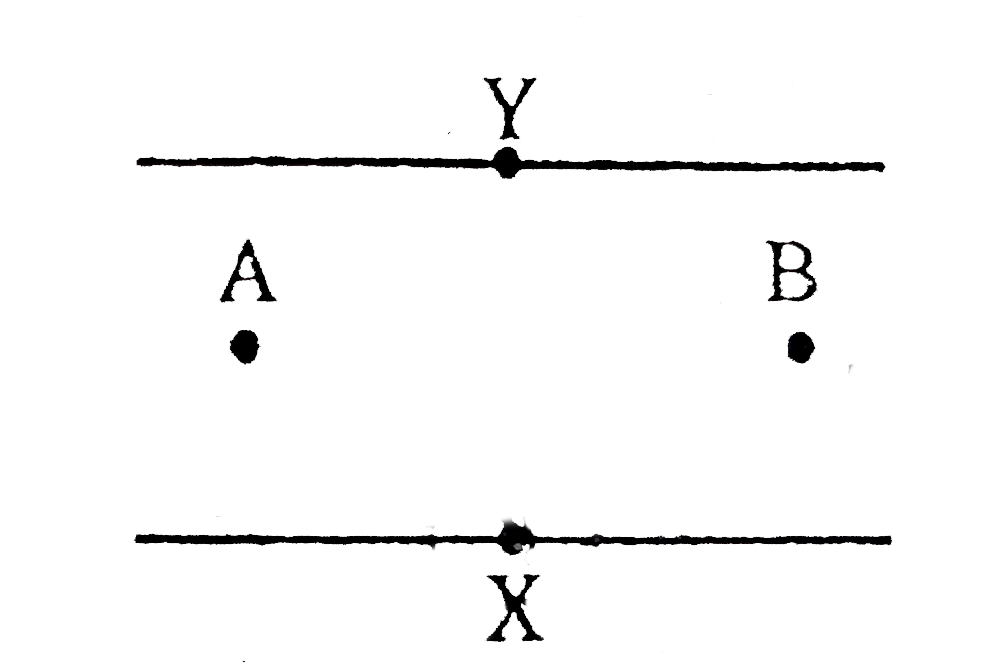
water is still, the person will take a time 30 minute in swimming from A to B and back to A along the shortes path. But we know that water is acually not still. The person also knows the technique of just flowing with water without exerting his own effort. Using this technique, i.e., just being carried with water, he takes a time 20 minute in moving from A to B. As shown, X and Y are two places directly oppsite to each other on oppsite banks. Assuming that width of the river is the same as the distance A and B, answer these questions. (assume v>vw)
Choose the correct option(s) :A60√12minB60√5minC60√2minD60√7min
Arjun takes 5 hrs to swim a upstream of 40km where as he takes only 2 hrs to swim downstream of 24km. Find the speed in still water.
A)15 kmph
B)10 kmph
C)12kmph
D)9kmph
View SolutionA and B are two fixed spots in a river in which water has a steady sped vw. A person who can swim with a speed v relative to water swims from A to B and back to A alomg shortest path. If the
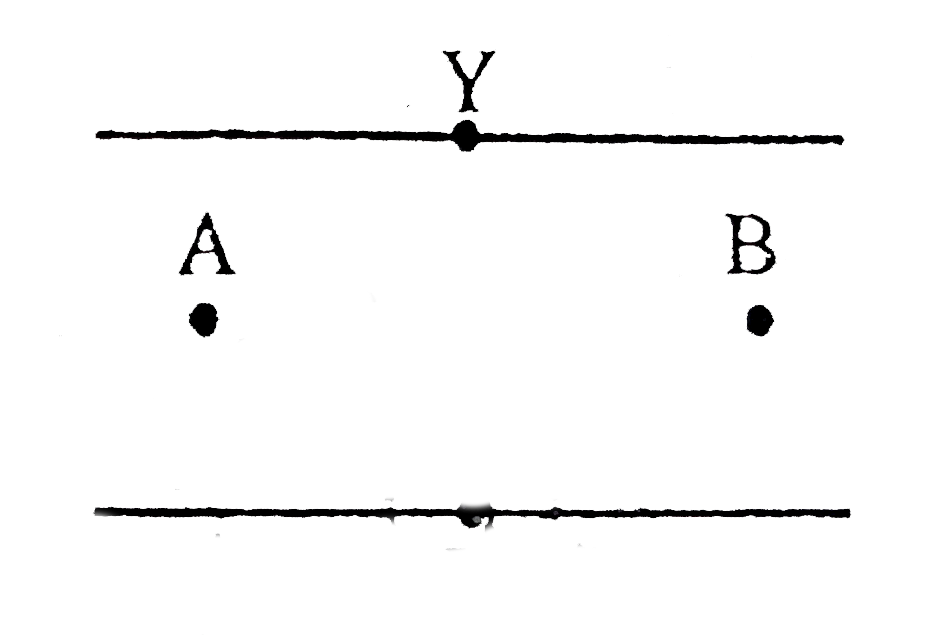
water is still, the person will take a time 30 minute in swimming from A to B and back to A along the shortes path. But we know that water is acually not still. The person also knows the technique of just flowing with water without exerting his own effort. Using this technique, i.e., just being carried with water, he takes a time 20 minute in moving from A to B. As shown, X and Y are two places directly oppsite to each other on oppsite banks. Assuming that width of the river is the same as the distance A and B, answer these questions. (assume v>vw)
Choose the correct option(s) :
View SolutionTo cross the river in shortest distance, a swimmer should swimming an angle theta with the upsteram. What is the ratio of the time taken to swim across in the shortest time to that in swimming across over shortest distance. [Asume that the speed of swimmer in still water is greater than the speed of river flow]
View SolutionA motorboat goes from A to B and comes back located at bank of river. If speed of motor boat becomes double in still water, it take 20% of its original time to travel from A to B and B to A. Find speed of motor boat is how many times than speed of flow of river ?
View SolutionA and B are two fixed spots in a river in which water has a steady sped vw. A person who can swim with a speed v relative to water swims from A to B and back to A alomg shortest path. If the
water is still, the person will take a time 30 minute in swimming from A to B and back to A along the shortes path. But we know that water is acually not still. The person also knows the technique of just flowing with water without exerting his own effort. Using this technique, i.e., just being carried with water, he takes a time 20 minute in moving from A to B. As shown, X and Y are two places directly oppsite to each other on oppsite banks. Assuming that width of the river is the same as the distance A and B, answer these questions. (assume v>vw)
Choose the correct option(s) :
View Solution
