A current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with is now bent so that it now lies in the y-z plane.
The magnitude of magnetic moment now diminishes.
The magnetic moment does not change.
The magnitude of B at increases.
The magnitude of B at is unchanged.
The correct Answer is:a
Let the loop be carrying current is an anticlockwise direction.
The area vector of the loop will be along positive Z-direction. For a circular loop of radius R, carrying current I, themagnetic moment will be given by:

[Along positive Z - axis]
Now, half of the loop is bent in the Y-Z plane (part ACD).
So, the net magnetic moment of the loop will be equal to the sum of the two magnetic moments of parts ABD and ACD of the loop.
Magnetic moment of part ABD will be
[Along positive Z - axis]
Magnetic moment of part ACD will be
[Along positive X - axis]
Resultant magnetic moment will be
[ Along Z-X plane at an angle with X -axis]
Thus, the magnitude of magnetic moment diminishes.
The magnitude of at a point on the axis of loop at a distance from the centre of the loop lying in the X-Y plane is:
[towards positive Z - axis] ....(i)
The magnitude of at a point due to part ABD will be
[towards positive Z - axis ]
The resultant magnetic field at a point on the axis of loop at a distance Z from the centre will be:
....(ii)
For , from (i) and (ii) , we have
....(iii)
, it can be ignored in the denominator]
Also, ...(iv)
From (iii) and (iv) , we have
Here, option (a) is correct.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) Objective Questions (MCQ Type - II)
5 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) (Very Short Answer Type Questions )
5 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT FILE (NCERT Additional Exercises)
15 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A circular wire loop of radius R is placed in the X-Y plane with its centre at the origin. The loop carries a current I in the clockwise direction when viewed from a point on the positive Z-axis. A uniform magnetic field →B=B0(ˆi+√3ˆj2) exists in the region x>R√32. The magnitued of the magnetic force on the loop due to the magnetic field is B0IRn. The value of n is______________.
View SolutionA circular wire loop of radius R is placed in the x-y plane centered at the origin O. A square loop of side a(a<<R) having two turns is placed with its centre at =√3R along the axis of hte circular wire loop, as shown in figure. The plane of the square loop makes an angle of 45∘ with respect to the z-axis. If the mutual inductance between the loops is given bu μ0a22p/2R, then the value of p is
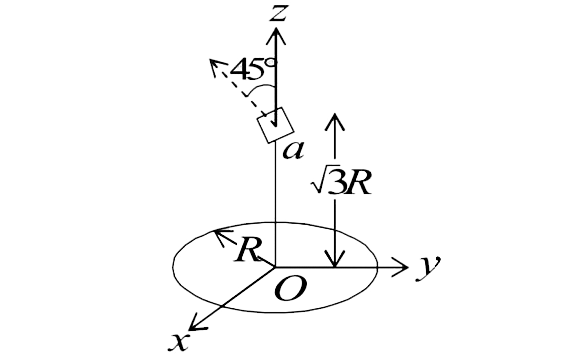
View Solution
Knowledge Check
A current − carrying circular loop of radius R is placed in the XY− plane with centre at the origin. Half of the loop with x>0 is now bent so that is now lies in the XY− plane
AThe magnitude of magnetic moment now diminishesBThe magnetic moment does not changeCThe magnitude of →B at (0,0,z),z>>R increeasesDThe magnitude of →B at (0,0,z),z>>R is unchangedA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.BzeroCinversely proportional to r.Ddirectly proportional to I.A circular loop of radius R, carrying I lies in xy-plane with its centre at origin. The total magnetic flux through xy-plane is :
Adirectly proportional to RBdirectly proportional to ICinversely proportional to RDzero
A circular loop of radius R, carrying I lies in xy-plane with its centre at origin. The total magnetic flux through xy-plane is :
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
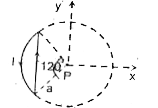
View SolutionA current carrying circular loop is freely suspended by a long thread. The plane of the loop will point in the direction
View SolutionA current carrying circular loop is freely suspended by a long thread. The plane of the loop will point in the direction
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View Solution
