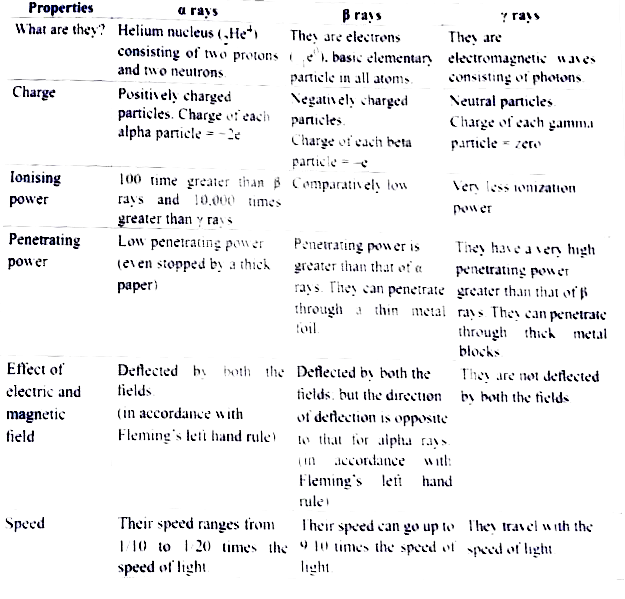
Compare the properties of alpha, beta, and gamma radiations.Solution in Tamil
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - FULL MARKSCHAPTER - NUCLEAR PHYSICSEXERCISE - TEXTUAL EVALUATION (XII. HOT Questions)
3 Videos
- NUCLEAR PHYSICSBOOK - FULL MARKSCHAPTER - NUCLEAR PHYSICSEXERCISE - Additional Questions (I. Choose the best Answer)
40 Videos
- NUCLEAR PHYSICSBOOK - FULL MARKSCHAPTER - NUCLEAR PHYSICSEXERCISE - TEXTUAL EVALUATION (X. Answer the following questions in few sentences)
9 Videos
- LAWS OF MOTIONBOOK - FULL MARKSCHAPTER - LAWS OF MOTIONEXERCISE - Additional Questions (VIII. Problems.)
2 Videos
- OPTICSBOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - ADDITIONAL QUESTIONS (VII. Give the Answer in detail)
3 Videos
Similar Questions
Mass number of a radioactive element is 232 and its atomic number is 90. When this element undergoes certain nuclear reactions, it transforms into an isotope of lead with a mass number 208 and an atomic number 82. Determine the number of alpha and beta dacay that can occur.
View SolutionRadium was discovered by
View SolutionWrite any three features of natural and artificial radioactivity.
View SolutionA cricket ball of mass 0.5 kg strikes a bat normally with a velocity of 30 ms−1 and rebounds with a velocity of 20 ms−1 in the opposite direction, calculate the impulse of the force exerted by the ball on the bat.
View SolutionState the laws of refraction
View SolutionUsing properties of determinants, prove the following ∣∣ ∣ ∣∣αβγα2β2γ2β+γγ+αα+β∣∣ ∣ ∣∣=(α−β)(β−γ)(γ−α)(α+β+γ)
View Solutionसारणिकों के गुणधर्मो का प्रयोग करके निम्नलिखित 11 से 15 तक प्रश्नो को सिद्ध कीजिए
∣∣ ∣ ∣∣αα2β+γββ2γ+αγγ2α+β∣∣ ∣ ∣∣=(β−γ)(γ−α)(α−β)(α+β+γ)
View SolutionCompare the properties of alpha, beta, and gamma radiations.
View Solutionα एवं β किरणों के गुणों की तुलना कीजिए ।
View SolutionUsing properties of determinants in Exercises prove that :
⎡⎢ ⎢⎣αα2β+γββ2γ+αγγ2α+β⎤⎥ ⎥⎦=(β−γ)(γ−α)(α−β)(α+β+γ)
View SolutionUsing properties of determinants in Exercises prove that :
∣∣(α,α2,β+γ),(β,β2,γ+α),(γ,γ2,α+β)|}=(β−γ)(γ−α)(α−β)(α+β+γ)
View SolutionUsing properties of determinants prove that :
∣∣(α,α2,β+γ),(β,β2,γ+α),(γ,γ2,α+β)|}=(β−γ)(γ−α)(α−β)(α+β+γ)
View SolutionUsing properties of determinants in Exercises prove that :
⎡⎢ ⎢⎣αα2β+γββ2γ+αγγ2α+β⎤⎥ ⎥⎦=(β−γ)(γ−α)(α−β)(α+β+γ)
View SolutionUsing properties of determinants. Prove that∣∣ ∣ ∣∣αα2β+γββ2γ+αγγ2α+β∣∣ ∣ ∣∣=(β−γ)(γ−α)(α−β)(α+β+γ)
View SolutionUsing properties of determinants in Exercise 11 to 15 prove that
∣∣ ∣ ∣∣αα2β+γββ2γ+αγγ2α+β∣∣ ∣ ∣∣=(β−γ)(γ−α)(α+β+γ)(α−β)
View SolutionUsing properties of determinants, prove that
∣∣ ∣ ∣∣αα2β+γββ2γ+αγγ2α+β∣∣ ∣ ∣∣=(β−γ)(γ−α)(α−β)(α+β+γ)
View Solution