A Proton moves in a iniform magnetic field of strength 0.500 T magnetic field is directed along the x-axis . At initial time, t = 0 s, the proton has velocity →v=(1.95×105ˆi+2.00×105ˆk)ms−1. Find
(a) At initial time, what is the acceleration of the proton
(b) is the path circular or helical , calculate the radius of helical trajectory and also calculate the pitch of the helix (Note: Pitch of the helix is the distance travelled along the helix axis per revolution ). Solution in Tamil
Magnetic field →B=0.500ˆi T
Velocity of the particle →v=(1.95×105ˆi+2.00×105ˆk)mas−1
Charge of the proton q = 1.60 ×10−19 C
Mass of the proton m = 1.67×10−27kg
(a) the force experienced by the proton is →Fq(→v×→B)
= 1.60×10−19×((1.95×105ˆi+2.00×105ˆk)×(0.500ˆi))
Therefore, from Newton.s second law,
→a=lm→F=l1.67×10−27(1.60×10−14)
= 9.58 ×1012ms−2
(b) Trajectory is helical
Radius of helical path is
R=mvz|q|B=1.67×10−27×2.00×1051.60×10−19×0.500=4.175×13−3m=4.18 mm
Pitch of the helix is the distance travelled along x-axis in a time T, which is P = vx T But time,
T=2πω=2πm|q|B=2×3.14×1.67×10−271.60×10−19×0.500=13.1×10−8s
hence , pitch of the helix is
P=vxT=(1.95×104)(13.1×10−8)=25.5×10−3m=25.5mm
The proton experiences appreciable acceleration in the magnetic field, hence the pitch of the helix is almost six times greater than the radius of the helix.
Topper's Solved these Questions
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - TEXT EVALUATION SOLVED
15 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT BOOK - FULL MARKSCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT EXERCISE - TEXT EVALUATION SOLVED -SHORT ANSWER QUESTIONS
10 Videos
- ELECTROSTATICS BOOK - FULL MARKSCHAPTER - ELECTROSTATICS EXERCISE - ADDITIONAL QUESTIONS SOLVED ( VII. NUMERICAL PROBLEMS )
5 Videos
- OPTICSBOOK - FULL MARKSCHAPTER - OPTICSEXERCISE - ADDITIONAL QUESITON - II ADDITIONAL PROBLEMS:
11 Videos
Similar Questions
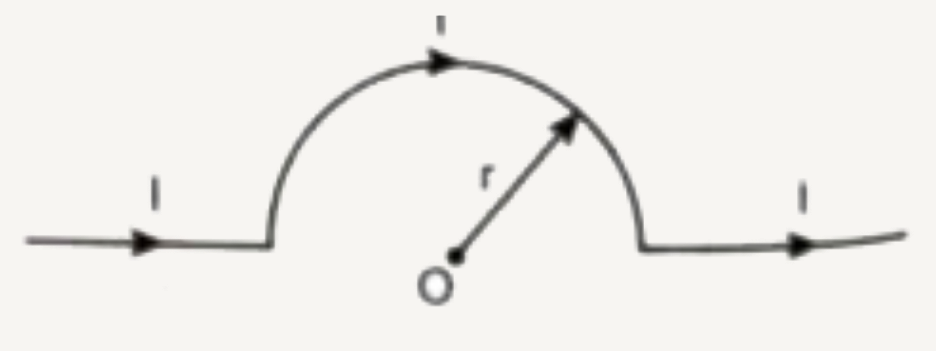
The magnetic field at the center O of the following current loop is ............ .
View SolutionWhat is meant by magnetic induction ?
View SolutionElectrons are caused to fall through a potential difference of 1500 volts. If they were initially at rest. Then calculate their final speed.
View SolutionLight from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm ). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
View SolutionA beam of protons moving with a velocity of 4×105ms enetrs a uniform magnetic field of 0.3 T at an angle of 60◦ with the magnetic field. What is the radius of the helical path described by the proton beam?[mp=1.67×10−27kg and the charge on the proton=1.6×10−19C]
View SolutionA proton is traveling along the X - direction with velocity 5×106 ms−1 . The magnitude of force experienced by the proton in a magnetic field.
→B=(0.2ˆi+0.4ˆk) telsa is
View SolutionA magnetic field of →B=1×10−2ˆk tesla applies a force of →F=(36ˆI+12ˆj)×10−23 newton on a proton. Calculate the velocity of proton.
View SolutionAn α particle is moving with a velocity of (7×105ˆIm/s) in a magnetic field of (5ˆI+9ˆj) T. Find the magnetic force acting on the particle.
View SolutionAn α particle is moving with a velocity of (7×105ˆim/s) in a magnetic field of (5ˆi+9ˆj). T . Find the magnetic force acting on the particle.
View SolutionA beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helical path taken by the proton beam.
View SolutionA beam of protons moving with a velocity of 4 xx 10^(5) m/s enters a uniform magnetic field of 0.3 T at an angle of 60◦ with the magnetic field. What is the radius of the helical path described by the proton beam? [m_p=1.67 xx 10^(-27) kg and the charge on the proton =1.6 xx 10^(-19) C]
View SolutionA proton is projected with a speed of 2 xx 10^(5) m/s at an angle 60^(circ) to x -axis. If a uniform magnetic field of 0.1 T is 'applied along y -axis, then the path of proton is helical with time period a times 10^(-5) s . Find a . (Take pi=3.14)
View SolutionA proton which carries a charge of 1.6×10−19C moving with a velocity of 2×109ms−1 along the direction of a uniform magnetic field of 250 T. Calculate the force acting on the proton.
View SolutionA proton of velocity (3ˆi+2ˆj)ms−1 enters a field of magnetic induction (2ˆj+3ˆk) tesla . The acceleration producted in the proton in ms−2 is (specific charge or proton =0.96×108Ckg−1)
View SolutionThe magnetic field in a certain region of space is given by →B=8.35×10−2 T. A proton is shot into the field with velocity →v=(2×105ˆi+4×105ˆj) m/s. The proton follows a helical path in the field. The distance moved by proton in the x-direction during the period of one revolution in the jz-plane will be (Mass of proton =1.67×10−27kg)
View Solution
