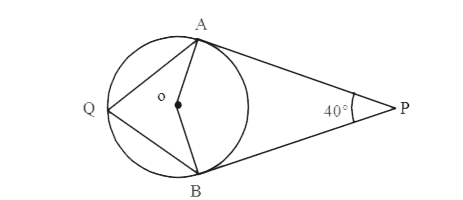
 If ABCD is a square incribed in a circle and PA is a tangent, then the angle between the lines P'A and P'B is _________.
If ABCD is a square incribed in a circle and PA is a tangent, then the angle between the lines P'A and P'B is _________.
30∘
20∘
40∘
45∘
The correct Answer is:D
Apply 'alternate segment theorem '.
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -2
17 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -3
15 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Essay type questions
3 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
Knowledge Check
O is the centre on the circle. PA and PB are tangent segments. Then the quadrilateral AOBP is :
ARectangleBSquareCCyclicDNone of theseP is a variable point on the curve y= f(x) and A is a fixed point in the plane not lying on the curve. If PA2 is minimum, then the angle between PA and the tangent at P is
Aπ4Bπ3Cπ2DNone of theseIn a given figure, if θ=50∘andPAandPB be the tangent lines, then ∠AQB is equal to
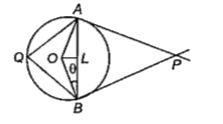 A40∘B50∘C60∘D70∘
A40∘B50∘C60∘D70∘
From an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D which intersect PA and PB at point E and C respectvely. If AP=15 cm, find the permeter of the △PEC.
View SolutionA square is incribed in a circle . If p1 is the probability that a randomly chosen point of the circle lies within the square and p2 is the probability that the point lies outside the square then
View Solution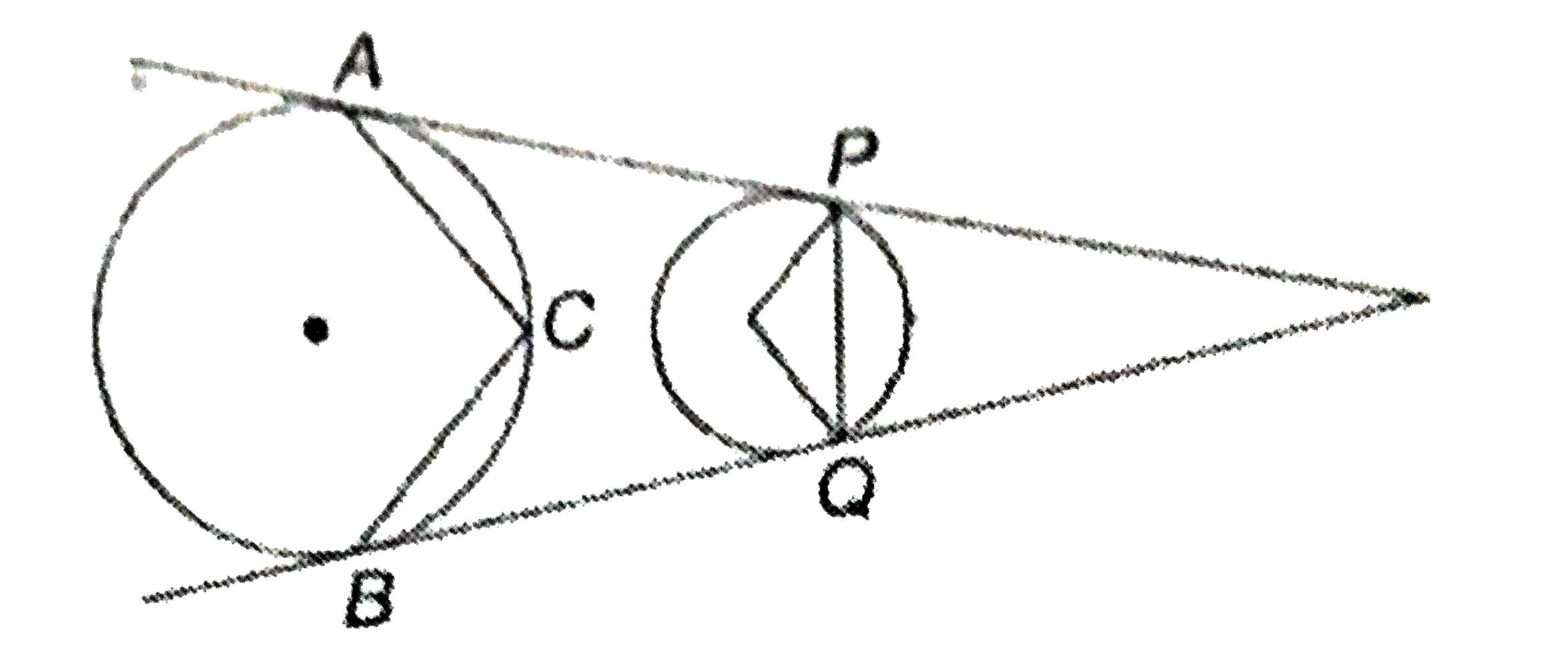
In the diagram above, A,B,P and Q are points of contacts of direct common tangents of the two circles. If ∠ACB is 120∘ , then find the angle between the two tangents and angle made by PQ at the centre of same circle.
View SolutionFrom an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
View SolutionA vertical pole PO is standing at the centre O of a square ABCD. If AC subtends an angle of 90∘ at the top , P of the pole, then the angle subtended by a side of the square at P is
View Solution