Find the sum of an infinite geometric series whose first term is and whose common ratio is the value of .
[Note : where {y} denotes fractional part of y.]
Video Solution
Text Solution
Therefore common ratio is
|
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION - 1 [PARAGRAPH TYPE]
4 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS SECTION - 1 [MULTIPLE CORRECT CHOICE TYPE]
6 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION-3 PART-B [MULTIPLE CORRECT CHOICE TYPE]
5 Videos
- PROBABILITYBOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions
1 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column
7 Videos
Similar Questions
Knowledge Check
What is the value of limx→0x2sin(1x)?
A0B1C1/2DLimit does not existThe value of Limx→0(5x2+[x2+1])(1x2+sin2x) is,
[Note : [y] denotes greatest interger less than or equal to y.]A52Be52C252De252The value of limx→0(3√x3+2x2−√x2+x) is
AeBe2Csqrt€De−1
Let sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
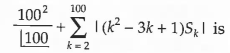 is
is
View SolutionThe value of limx→0e−(1+x)1/xtanx is
View SolutionFind the sum of the infinite geometric series 1+3x+9x2+27x3+…..
View SolutionFind the sum of an infinite geometric series whose first term is the limit of the function f(x)=tanx−sinxsin3x as x→0 and whose common ratio is the limit of the function g(x)=1−√x(cos−1x)2 as x->1
View SolutionThe value of limx→0sin−1{x} (where {.} denotes fractional part of x) is
View Solution
