In the adjacent figure a parabola is drawn to pass through the vertices B,C and D of the square ABCD. If A(2,1),C(2,3), then focus of this parabola is

(1,114)
(2,114)
(3,134)
(2,134)
The correct Answer is:B
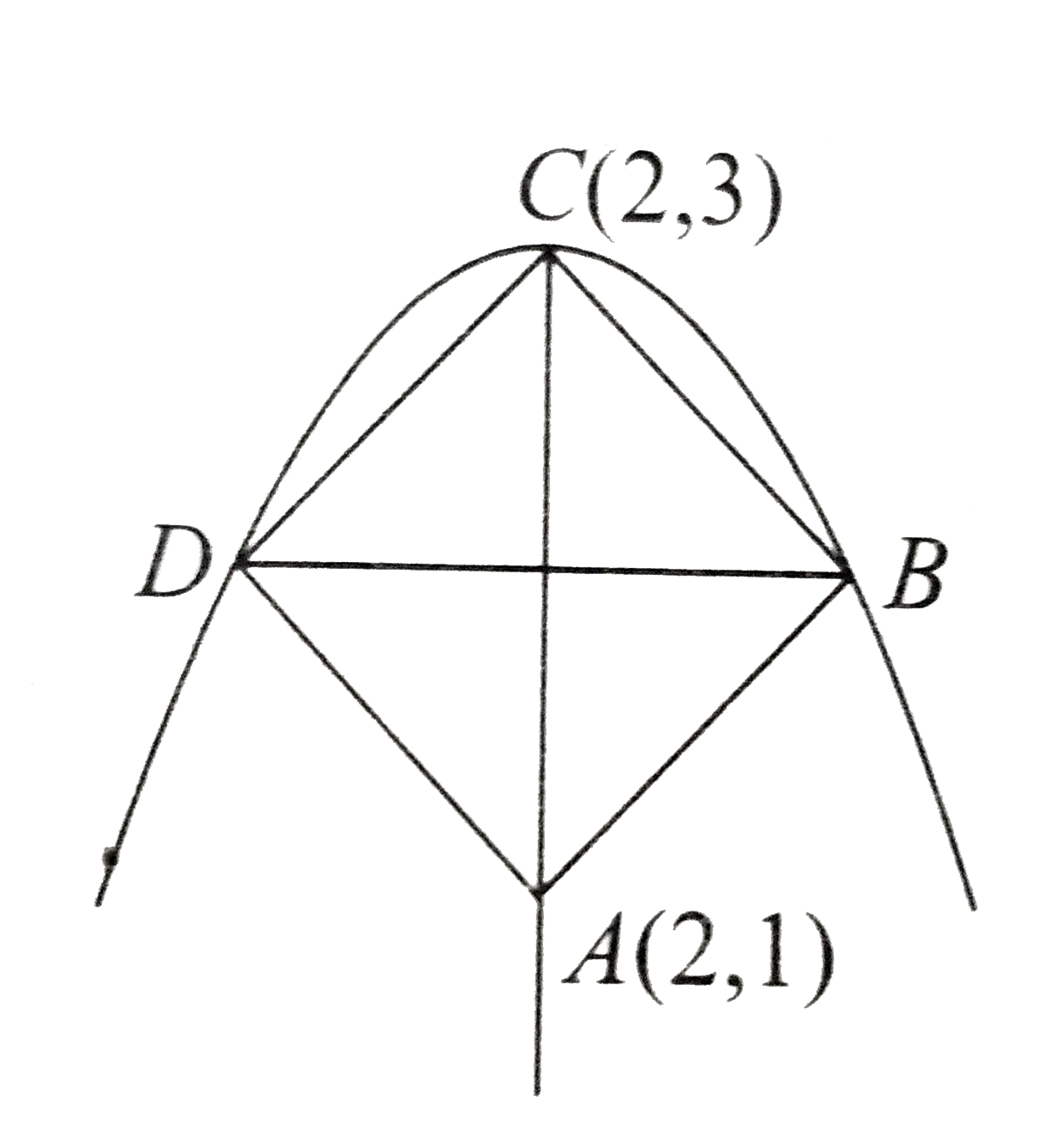
AC is parallel to y-axis and its mid-point is (2,2). Thus, B≡(3,2) and D≡(1,2).
Equation of parabola,
(x−2)2=λ(y−3)
It passes through (3,2), so
1=−λ⇒λ=−1
∴(x−2)2=−(y−3)
Hence, axis is x−2=0,L.R. line is y−3=−14
∴ Focus ≡(2,114)
Topper's Solved these Questions
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type
10 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Comprehension Type
2 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - JEE Advenced Single Answer Type
18 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank
19 Videos
Similar Questions
Focus of parabola y=ax2+bx+c is
View SolutionA square has one vertex at the vertex of the parabola y2=4ax and the diagonal through the vertex lies along the axis of the parabola. If the ends of the other diagonal lie on the parabola, the coordinates of the vertices of the square are (a)(4a,4a) (b) (4a,−4a) (c)(0,0) (d) (8a,0)
View Solution
Knowledge Check
The equation of the parabola passes through the parabola (1,1) and (2,4)
Ay2=xBx2=yCx2=4yDy2=4xA parabola is drawn with focus at (3,4) and vertex at the focus of the parabola y2−12x−4y+4=0. The equation of the parabola is
Ax2−6x+8y+25=0By2−8x−6y+25=0Cx2−6x+8y−25=0Dx2+6x−8y−25=0A parabola is drawn with its focus at (3,4) and vertex at the focus of the parabola y2−12x−4y+4=0. The equation of the parabola is
Ay2−8x−6y+25=0By2−6x+8y−25=0Cx2−6x−8y+25=0Dx2+6x−8y−25=0
If the parabola y2=ax passes through (1,2) then the equation of the directrix is
View SolutionNumber of distinct normals of a parabola passing through the focus of the parabola is
View SolutionA parabola passes through the point the point (1,2), (2,1), (3,4) and (4,3). Find the equation of the axis of parabola.
View SolutionThe focus of a parabola is (1,2) and the point of intersection of the directrix and axis is (2,3).Then the equation of the parabola is
View SolutionA square has one vertex at the vertex of the parabola y2=4ax and the diagonal through the vertex lies along the axis of the parabola. If the ends of the other diagonal lie on the parabola, the coordinates of the vertices of the square are (4a,4a) (b) (4a,−4a) (0,0) (d) (8a,0)
View Solution
