In an isosceles triangle ABC, the coordinates of the points Band C on the base BC are respectively (1,2) and (2.1). If the equation of the line AB is y=2x, then the equation of the line AC is

A

y=12(x−1)

B

y=x2

C

y=x−1

D

2y=x+3

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

∠ABC=tanθ=12−11+12=−13(m1=12,m2=1)
∵AB=AC,∴∠ABC=∠ACB
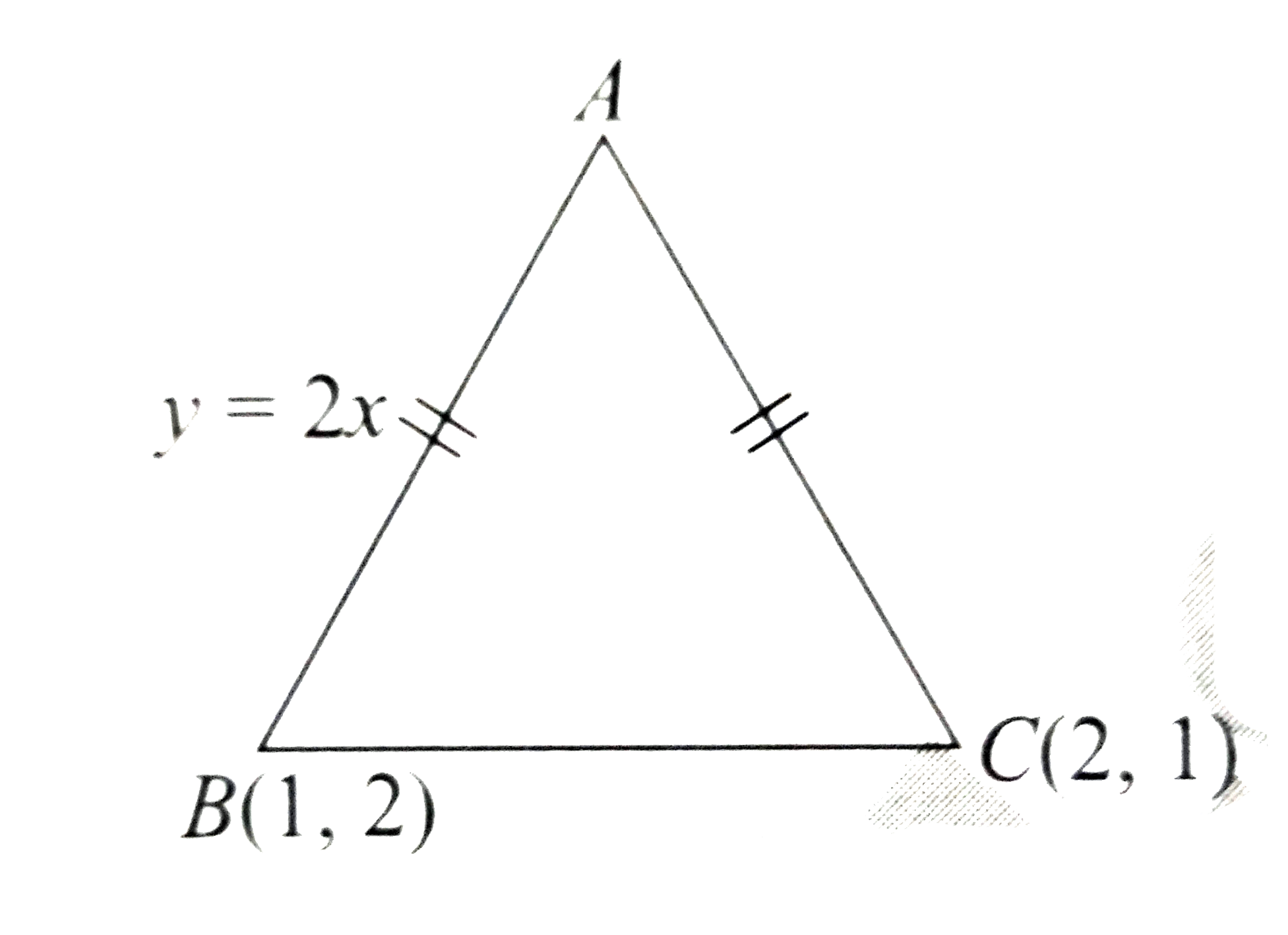
ocr_image
Hence, −13=m−11+m⇒m=12 (here m is the gradient of line AC)
∴ Equation of line AC is y−1=12(x−2)⇒y=x2

Updated on:21/07/2023
|
Class 12MATHSSTRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The coordinates of angular point of a Δ ABC are A(0,1), B(2,0) and C(-1,-2). Find the equation of side AB of the triangle.

    Ax-2y=1
    Bx + y = 2
    Cx + 2y = 2
    Dx + 3y = 1

  • ABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(-2,7), the coordinates of vertex A can be

    A(1,6)
    B(−1/2,5)
    C(−5/6,6)
    Dnone of these

  • ABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(-2,7), the coordinates of vertex A can be

    A(1,6)
    B(−12,5)
    C(56,6)
    D(−7,18)