The resultat of two rectangular simple harmonic motions of the same frequency and unequal amplitudes but differing in phase by π2 is : Solution in Kannada
simple harmonic
circular
elliptical
parabolic.
The correct Answer is:B
Step by step video, text & image solution for The resultat of two rectangular simple harmonic motions of the same frequency and unequal amplitudes but differing in phase by (pi)/(2) is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - MCQ (LEVEL-II)62videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - MCQ (LEVEL-III) Questions From AIEEE/JEE Examination10videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MOCK TEST-3EXERCISE - MCQs49videos
MOCK TEST-3
- BOOK - MODERN PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - RECENT COMPETITIVE QUESTIONS17videos
PROPERTIES OF MATTER
Similar Questions
A pendulum suspended from ceiling of a train has a time period T, when the train is at rest. When the train is accelerating with uniform acceleration 'a', the period of oscillation will
01:57View SolutionTwo particles are executing simple harmonic motion of the same amplitude A and frequency ω along the x-axis. Their mean position is separated by distance X0(X0>A). If the maximum separation between them is (X0+A), the phase difference between their motion is
03:46View SolutionA man standing in a lift holds a spring balance with a load of 5 kg suspended from it. What would be the reading of the balance when the lift is descending with an acceleration of 4ms−2 ?
01:51View SolutionWhich of the following substances has the highest elasticity ?
00:44View SolutionA particle is subjected to two simple harmonic motion in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions. Find the phase difference between the individual motions.
04:50View SolutionThe resultant of two rectangular simple harmonic motion of the same frequency and unequal amplitude but differing in phase by π/2 is
01:38View SolutionA particle is subjected to two simple harmonic motions in the same direction having equal amplitude and equal frequency. If the resultant amplitude is equal to the amplitude of individual motions, what is the phase difference between the motions.
04:53View SolutionTwo simple harmonic motions with the same frequency act on a particle at right angles i.e., along X-axis and Y-axis. If the two amplitudes are equal and the phase difference is pi//2 , the resultant motion will be
02:41View SolutionFind the phase different between two particles executing simple harmonic motion with the same amplitude and frequency when their phases at a certain moment are as shown in the figure.
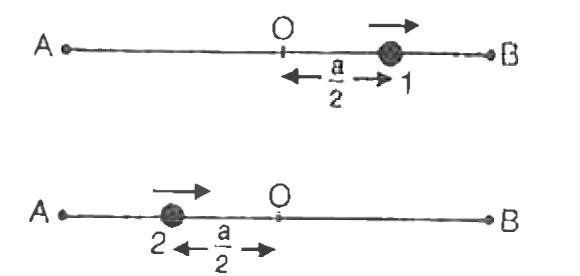 05:10View Solution
05:10View SolutionWhen two mutually perpendicular simple harmonic motions of same frequency, amplitude and phase are susperimposed
02:31View SolutionA particle is executing two different simple harmonic motions, mutually perpendicular, of different amplitudes and having phase difference of pi//2 . The path of the particle will be
02:59View SolutionTwo simple harmonic motions with the same frequency act on a particle at right angles i.e, along x and y axis. If the two amplitudes are equal and the phase difference is (pi)/(2) the resultant motion will be :
View SolutionWhat is the result of superposition of two collinear simple harmonic motions of the same frequency but of different amplitudes when they are (i) in the same phase and (ii) in opposite phase?
04:26View SolutionA particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions, find the phase difference between the individual motions.
02:35View SolutionA particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resulting amplitude is equal to the amplitude of individual motions, the phase difference between them is :
02:07View Solution
