The distance x covered by a body moving in a straight line in time is given by the relation 2 + 3x = t. If is the velocity of the body at a certain instant of time, its acceleration will be
−v3
−3v3
=2v3
−4v3
The correct Answer is:d
2x2+3x=t
Differetaiating both side w.r.t time,
∴4xdxdt+3dxdt=1
Since v=dxdt∴4xv+3v=1
(4x+3)v=1⇒4x+3=1v
⇒a=−4v21/v=−4v3
Topper's Solved these Questions
- DESCRIPTION OF MOTION IN ONE DIMENSION Book:MODERN PUBLICATIONChapter:DESCRIPTION OF MOTION IN ONE DIMENSION Exercise:MULTIPLE CHOICE QUESTION (LEVEL-II)
Explore 54 Videos
- DESCRIPTION OF MOTION IN ONE DIMENSION Book:MODERN PUBLICATIONChapter:DESCRIPTION OF MOTION IN ONE DIMENSION Exercise:Recent Competitive Question
Explore 12 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:RECENT COMPETITIVE QUESTIONS
Explore 32 Videos
- DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONBook:MODERN PUBLICATIONChapter:DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONExercise:Revision TEST
Explore 36 Videos
Similar Questions
Knowledge Check
A body moves in a straight line under the retardation a which is given by a=bv2. If the initial velocity is 2 m/s, the distance covered in time t=2 seconds is
Ab In (4)B1bIn(1+4b)Cb In (1-4b)D1bIn(4b−1)The velocity time graph of a body moving along a straight line is shown in figure. The ratio of the average velocities during the time t1 and t2 is.
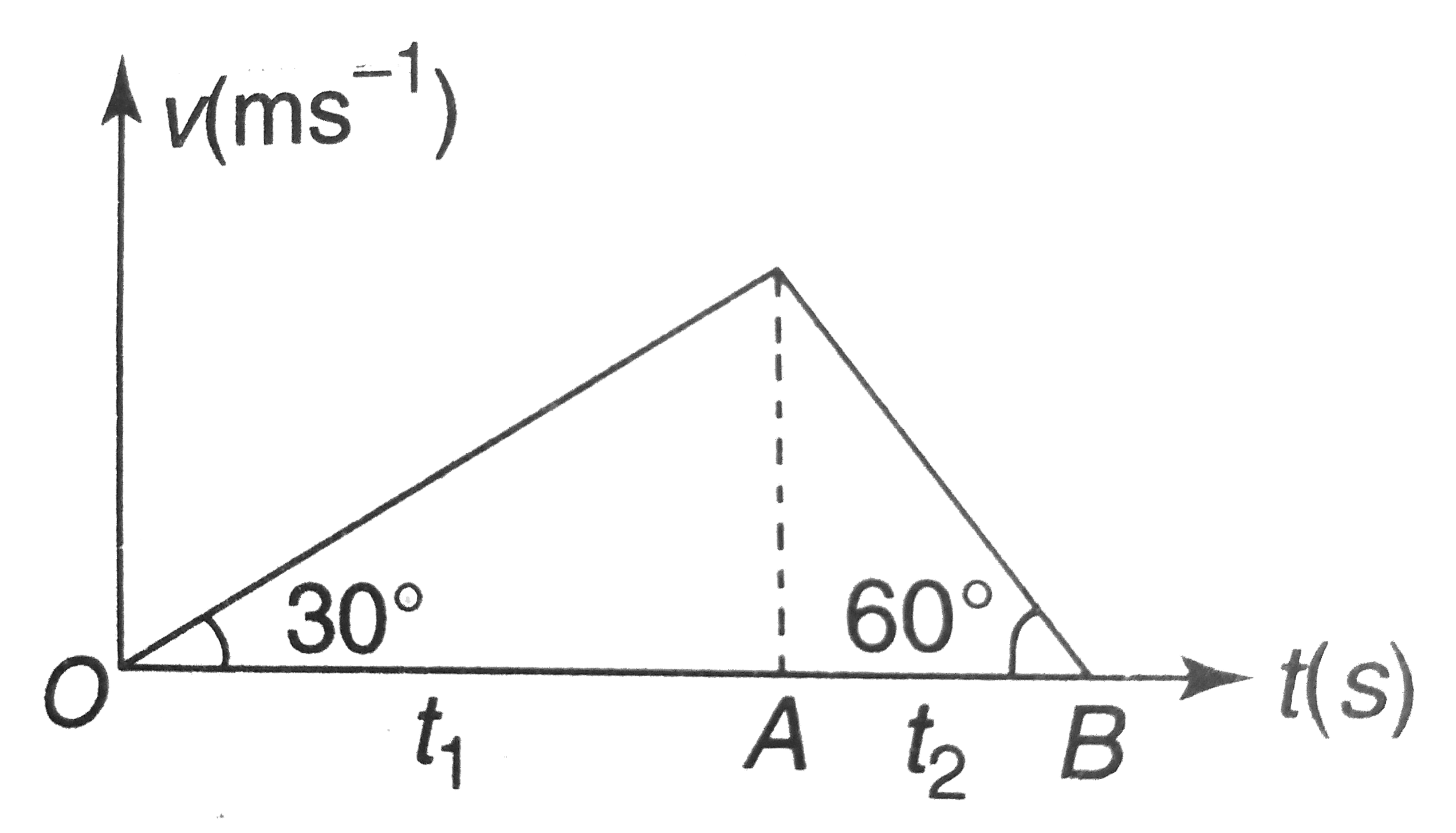 A1:1B2:1C3:1D1:3
A1:1B2:1C3:1D1:3The distance covered by a moving body is directly proportional to the square to the time. The acceleration of the body is
AincreasingBdecreasingCzeroDconstant
The coordinates of a body moving in a plane at any instant of time t are x=αt2 and y=βt2. The velocity of the body is
View SolutionThe velocity-time graph of a body moving in a straight line is shown in Fig. Find the displacement and distance travelled by the body in 10 sec.
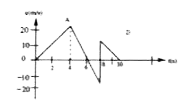
View SolutionThe distance covered by a moving body is directly proportional to the square to the time. The acceleration of the body is
View SolutionA body moves in a straight line along x-axis, its distance from the origin is given by the equation x=8t−3t2. The average velocity in the interval from t=0 to t=4 is
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
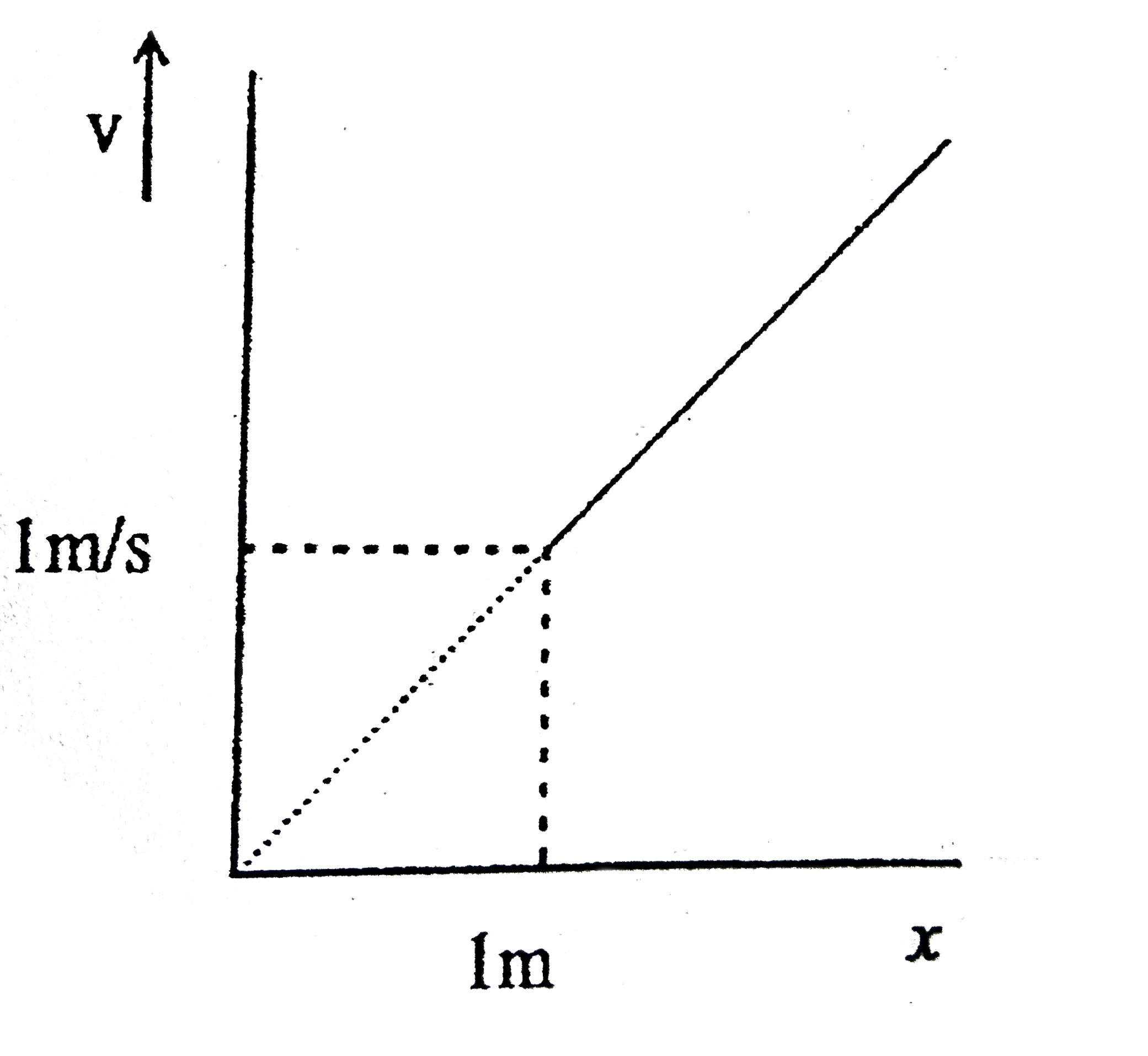
View Solution

