A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
the net elongation of the spring is 4πR3pg3k
the net elongation of the spring is 8πR3pg3k
the light sphere is partially submerged
the light sphere is completely submerged.
The correct Answer is:A, D
Sphere of density 3p will be below the sphere of density p as shown in figure. 
Forces acting on lower sphere are weight downwards, spring force upward and buoyant force upward. For equilibrium we can write the following
kx+43πR(2)(2p)g=43πR3(3p)g
Where x is a elongation of spring.
Solving above equation we get: x=4πR2pg3k.
Net downward forces (Spring fore and weight) acting on lighter body can be written as follows:
F=kx+43πR3pg
Substituting value of kx calculate above we get
F=43πR2(2p)g
Above calculated force is equal to byoyant force on lighter body when it is completely immersed, hence we can understant that for equilibrium lighter body will be completely immersed.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (D. MCQ Based On A Given Passage/Comprehension)
Explore 16 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (Assertion Reason Type Questions)
Explore 11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:MODERN PUBLICATIONChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Competition File (JEE (Advanced) For IIT Entrance)
Explore 14 Videos
- MATHEMATICAL TOOLSBook:MODERN PUBLICATIONChapter:MATHEMATICAL TOOLSExercise:PRACTICE PROBLEMS (10)
Explore 12 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
Similar Questions
A sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The electric field inside the sphere is
View SolutionA hollow sphere of external radius R and thickness t (< < R) is made of a metal of density ρ. The sphere will float in water if
View Solution
Knowledge Check
A sphere of radius R and density ρ1 is dropped in a liquid of density σ. Its terminal velocity is v1. If another sphere of radius R and density ρ2 is dropped in the same liquid, its terminal velocity will be:
A(ρ2−σρ1−σ)v1B(ρ1−σρ1−σ)v1C(ρ1ρ2)v1D(ρ2ρ1)v1
A solid hemisphere of radius R is made to just sink in a liquid of density ρ find theAπR3ρg3BπR3ρg2C0DπR3ρgWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
A105176R5ρB176105R5ρC105176R2ρD176105R2ρ
A solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
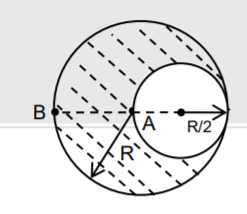
View SolutionIf ρ is density of the material of a sphere of radius R . Then its moment of inertia about its diameter is
View SolutionIn the figure shown, the heavy cylinder (radius R) reasting on a smooth surface separates two liquids of densities 2ρ and 3ρ. The height h for the equilibrium of cylinder must be
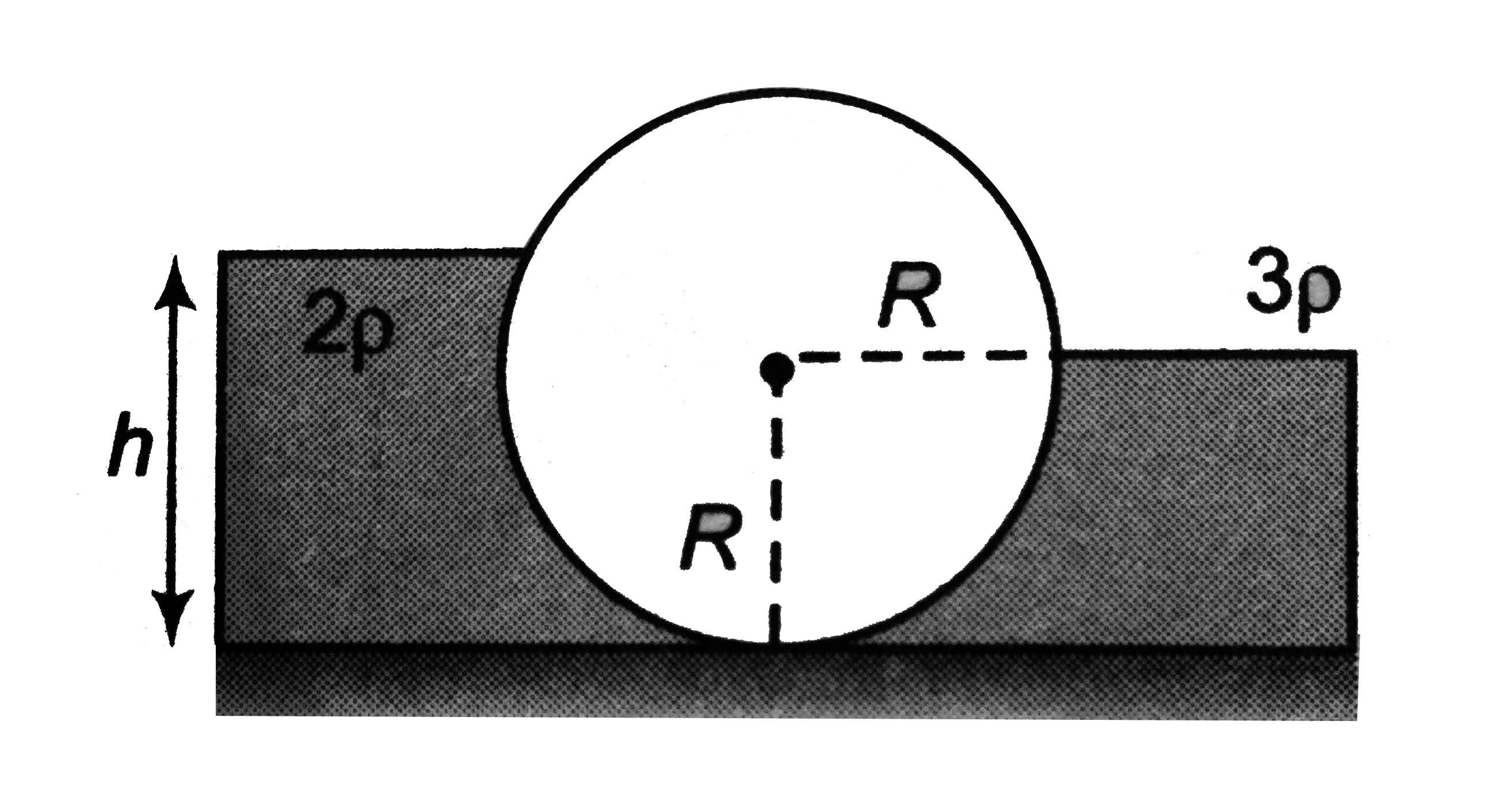
View SolutionA Solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid then density of liquid is– (r is distance from centre of sphere)
View SolutionWhat is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
View Solution

